-
a [[tool]]
- [[math]]
- [[wp]] https://en.wikipedia.org/Category_Theory
-
[[pull]] [[mini curriculum on applied category theory and engineering design]]
-
[[seven sketches in compositionality]] is an introductory book on category theory from a unique applied perspective
- At Cambridge University Press: https://www.cambridge.org/core/books/an-invitation-to-applied-category-theory/D4C5E5C2B019B2F9B8CE9A4E9E84D6BC
- ArXiv free version: https://arxiv.org/pdf/1803.05316.pdf
- Pirated final version: http://library.lol/main/C61E1736381D70DB2E3EE27829D00012
- MIT course on category theory and programming (bridging the math and programming ways of speaking) http://www.brendanfong.com/programmingcats.html
-
[[seven sketches in compositionality]] is an introductory book on category theory from a unique applied perspective
- [[pull]] [[category theory basics]]
-
#push [[category theory]]
- thought of [[graph]] / [[hypergraph]] as categories
- bought [[topoi]] by [[robert goldblatt]]
-
#push [[category theory]]
-
resources
- [[ncatlab]] ~ https://ncatlab.org
- papers
-
resources
-
#push [[Category Theory]]
-
Continuing reading [[A Rosetta Stone]]: https://via.hypothes.is/https://arxiv.org/pdf/0903.0340.pdf
- After 1.5y (!) -- time flies indeed.
-
Re-read [[cobordism]] as it keeps being hard to grasp :) I think I need to review more examples of the [[cobordism]] category?
- It's striking that one of the canonical representations of a cobordism looks like a pipe forking. Yesterday night I was reading/writing about [[flow networks]].
- Is category theory the study of change?
-
-
Continuing reading [[A Rosetta Stone]]: https://via.hypothes.is/https://arxiv.org/pdf/0903.0340.pdf
- [[push]] [[category theory]]
-
#push [[category theory]]
-
What if things [[isomorphic]] to each other are, in a way, near each other in the [[multiverse]]?
- If the fact that they are the same shape means they are near to each other in the [[library of babel]].
- Or the [[library of mendel]].
-
What if things [[isomorphic]] to each other are, in a way, near each other in the [[multiverse]]?
-
a [[class]]
- on [[2021-05-30]]
Idea of what [[category theory]] is. Basic definition of mathematical concepts.
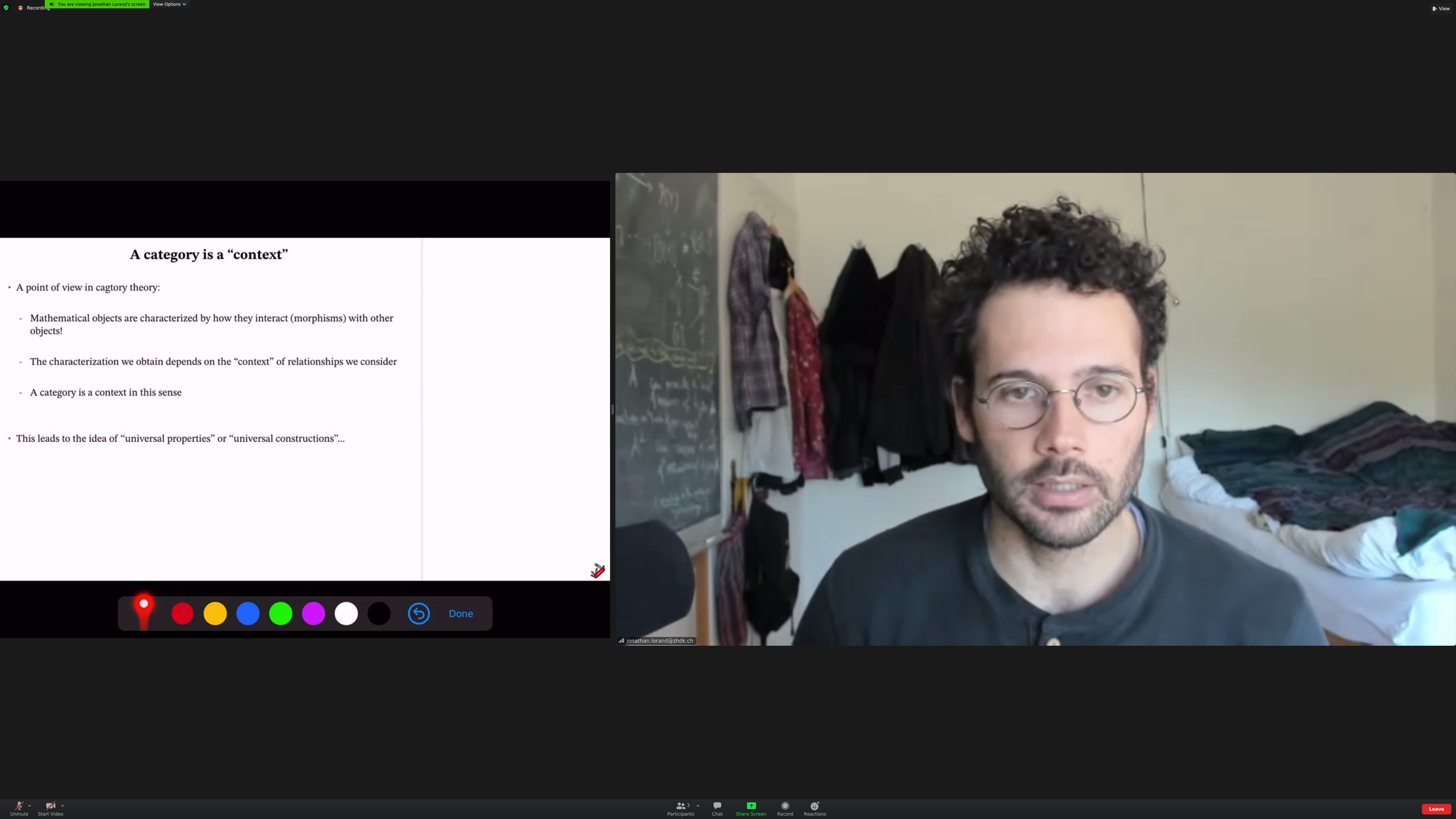
Notions that are important in category theory. Commutative diagrams; categories as kinds of [[context]]. At the end, how this fits in a bigger picture.
Aside: I'm reading Feynman and this fits in amazingly well with the introduction of that book, six easy pieces.
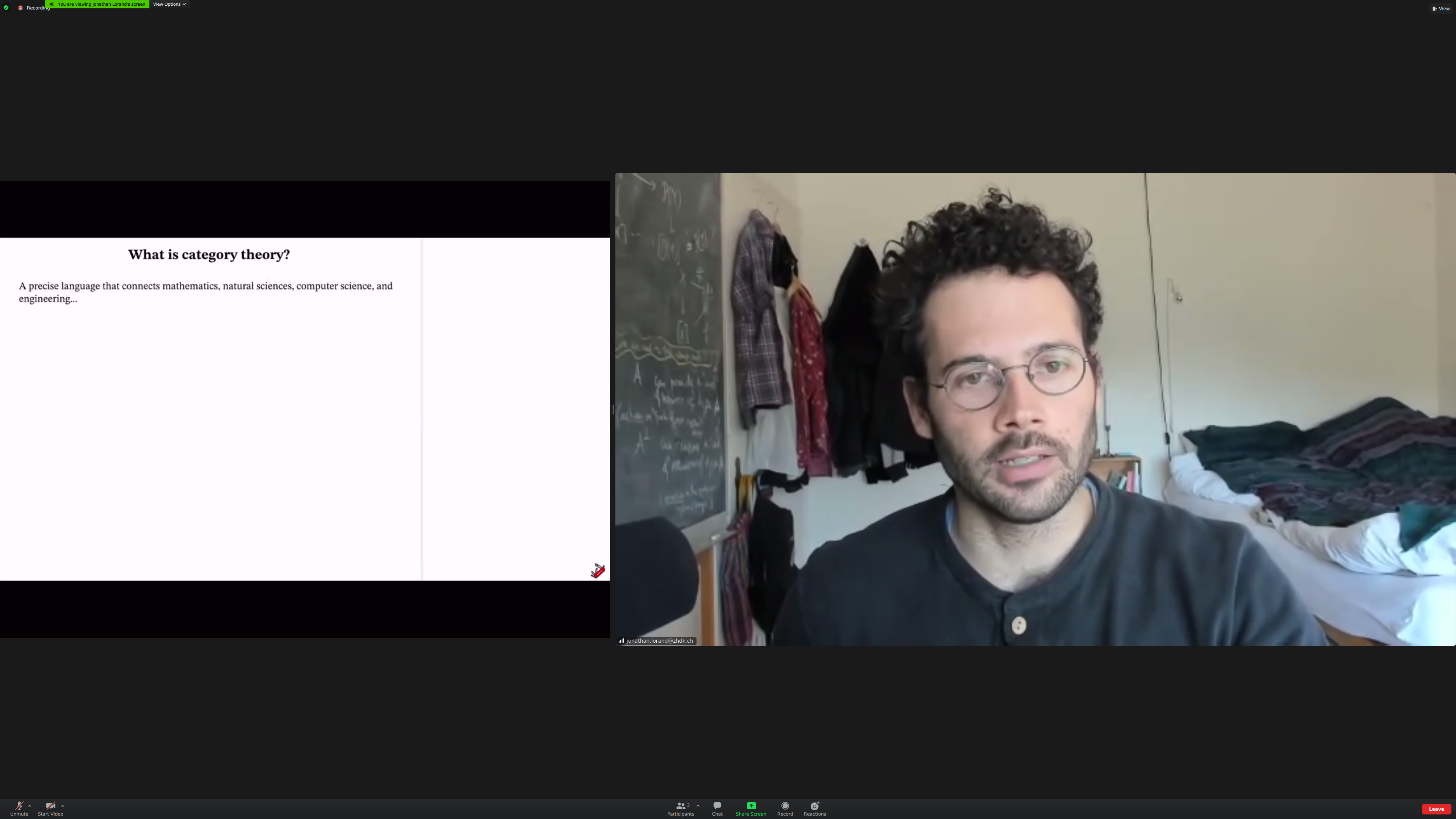
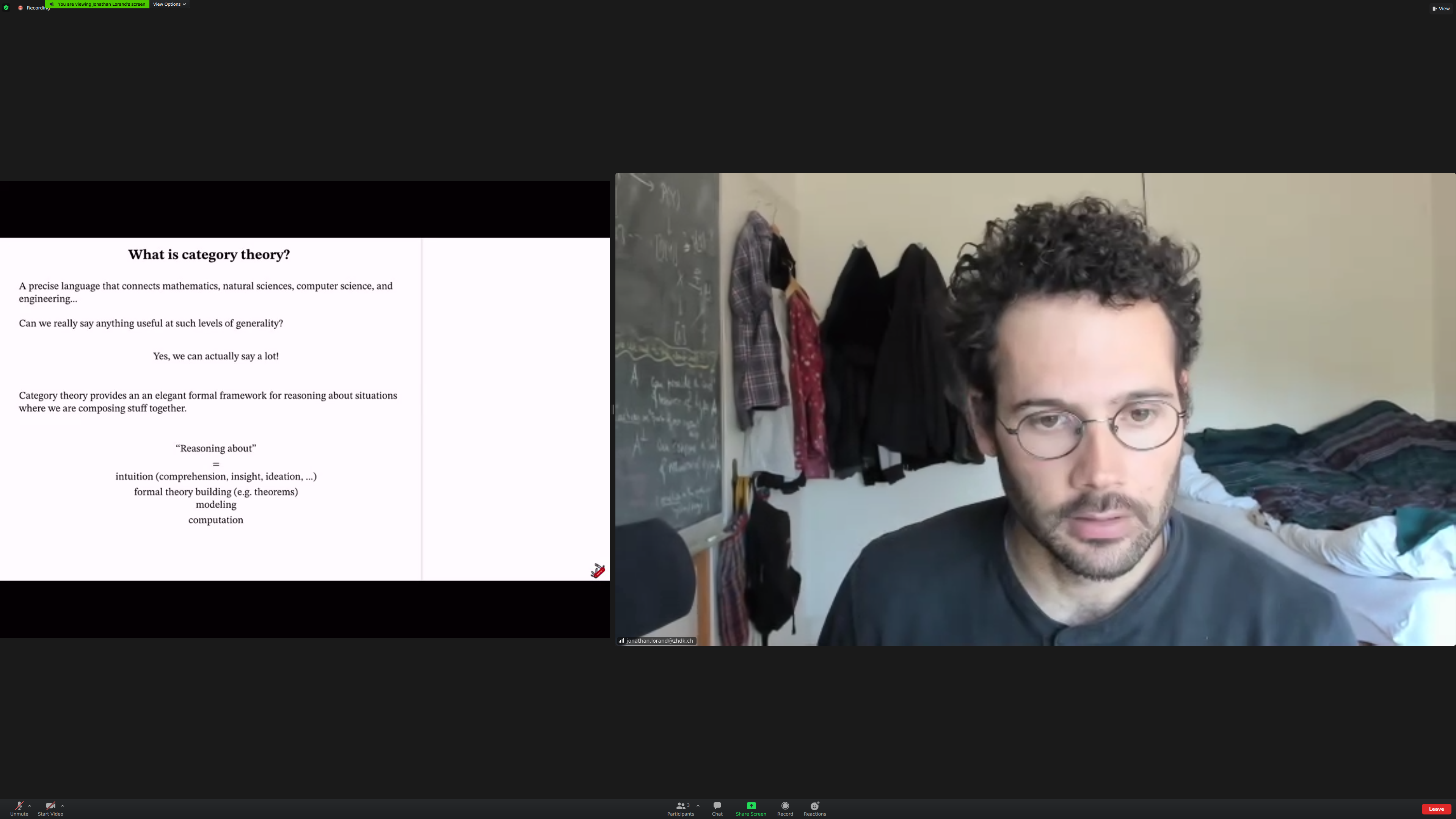
An [[elegant framework]] for reasoning about situations where we are composing stuff together. [[modeling]], [[computation]].
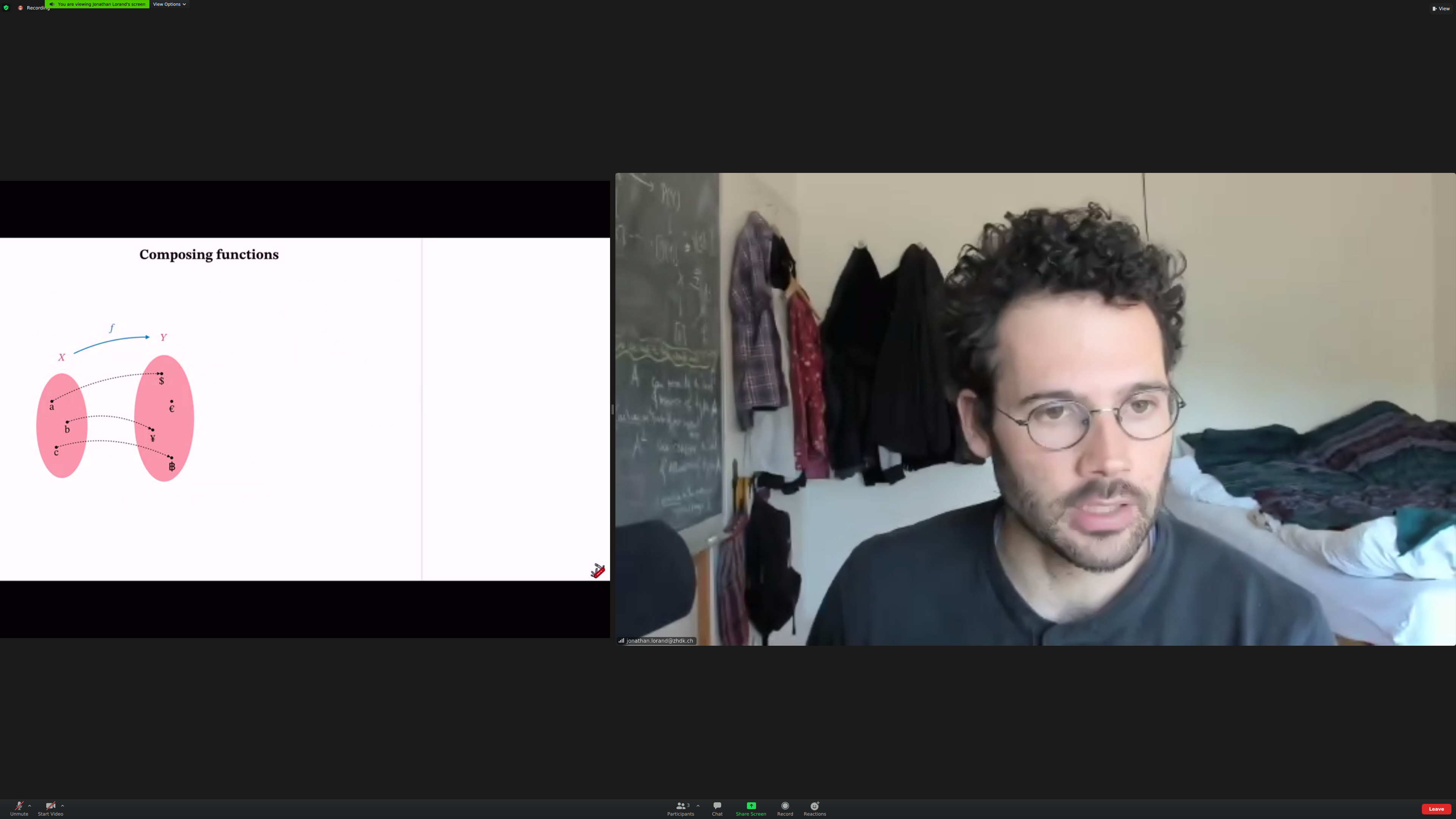
Category theory is about [[composing stuff]] together.
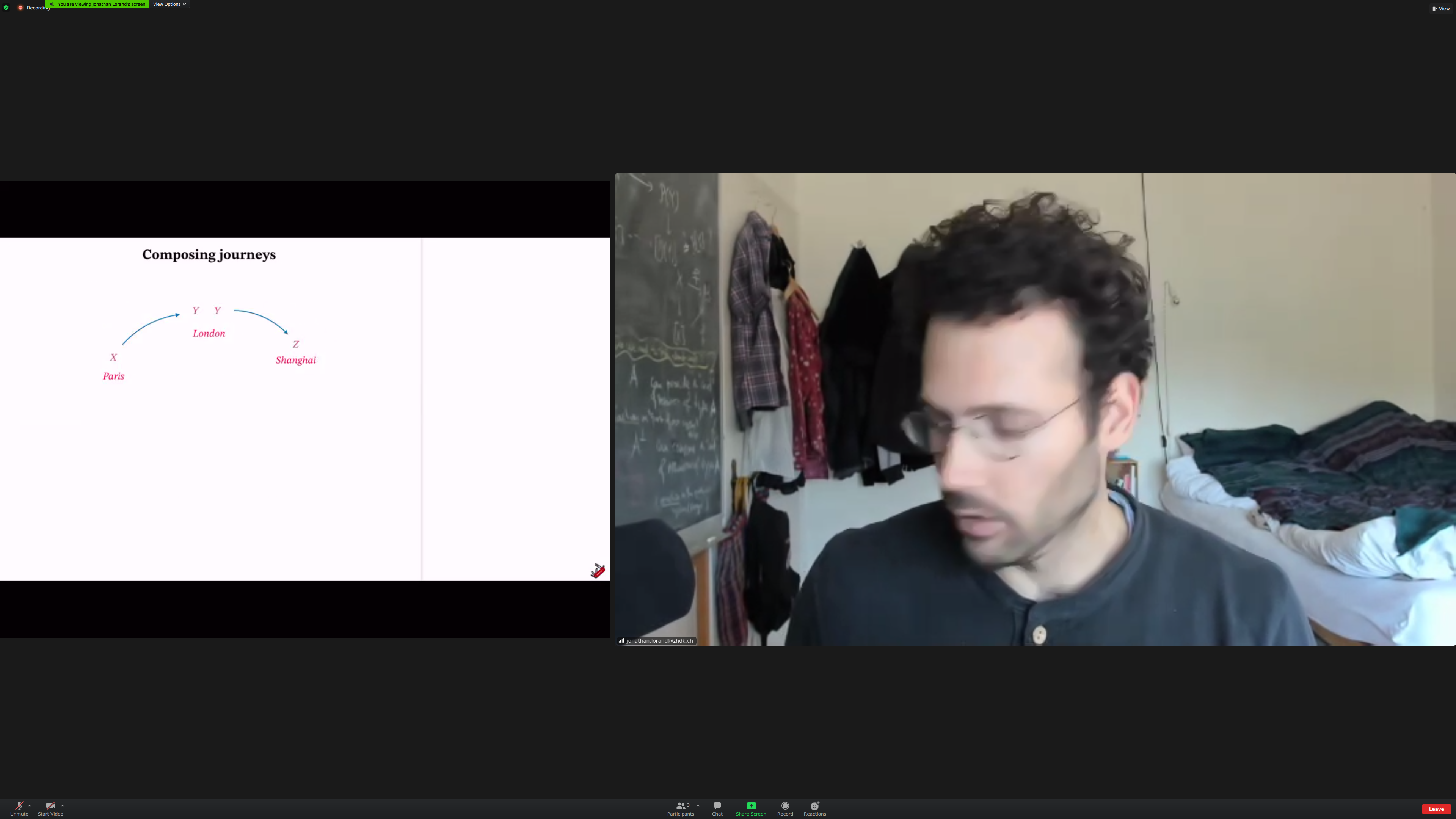
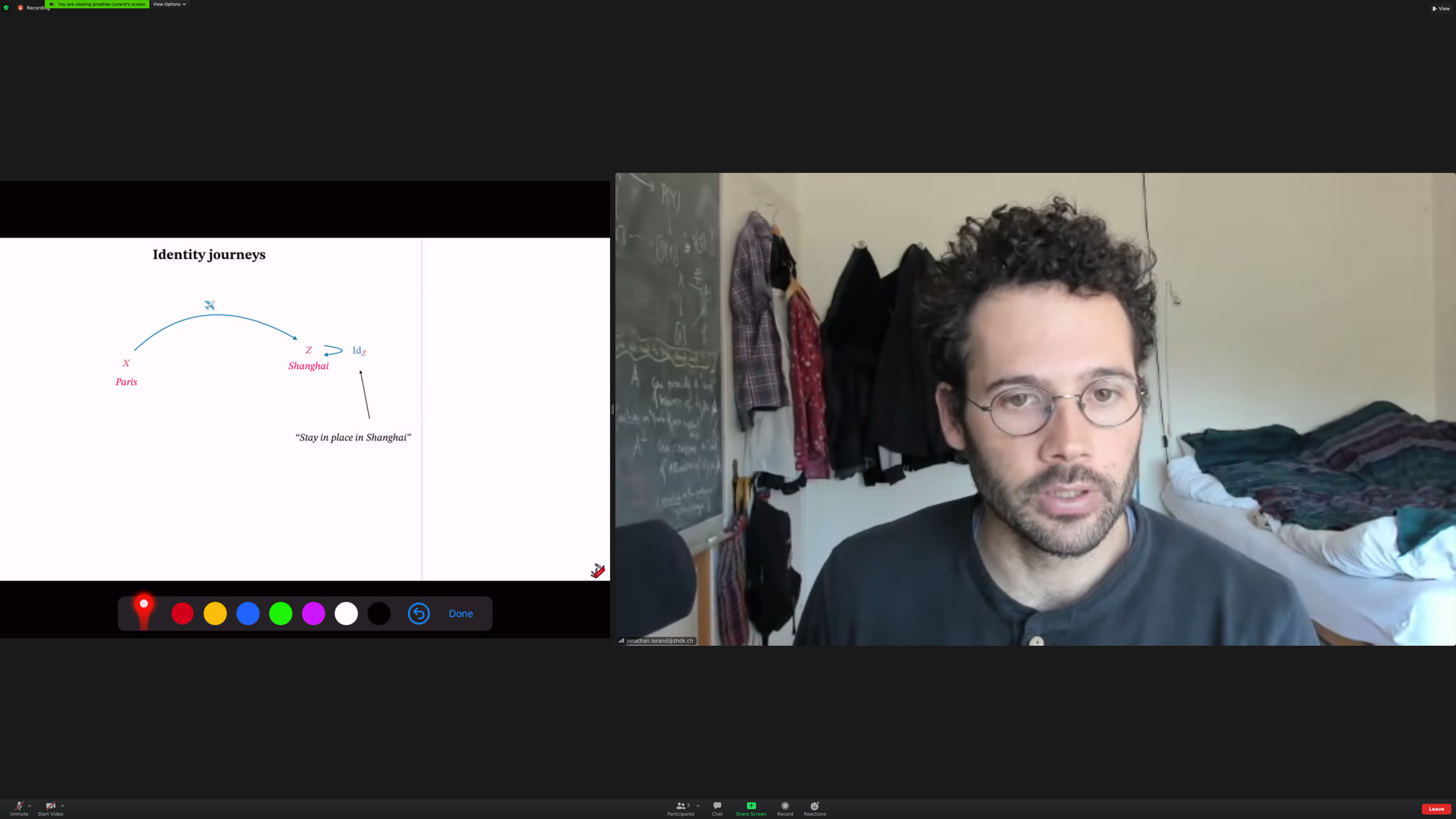
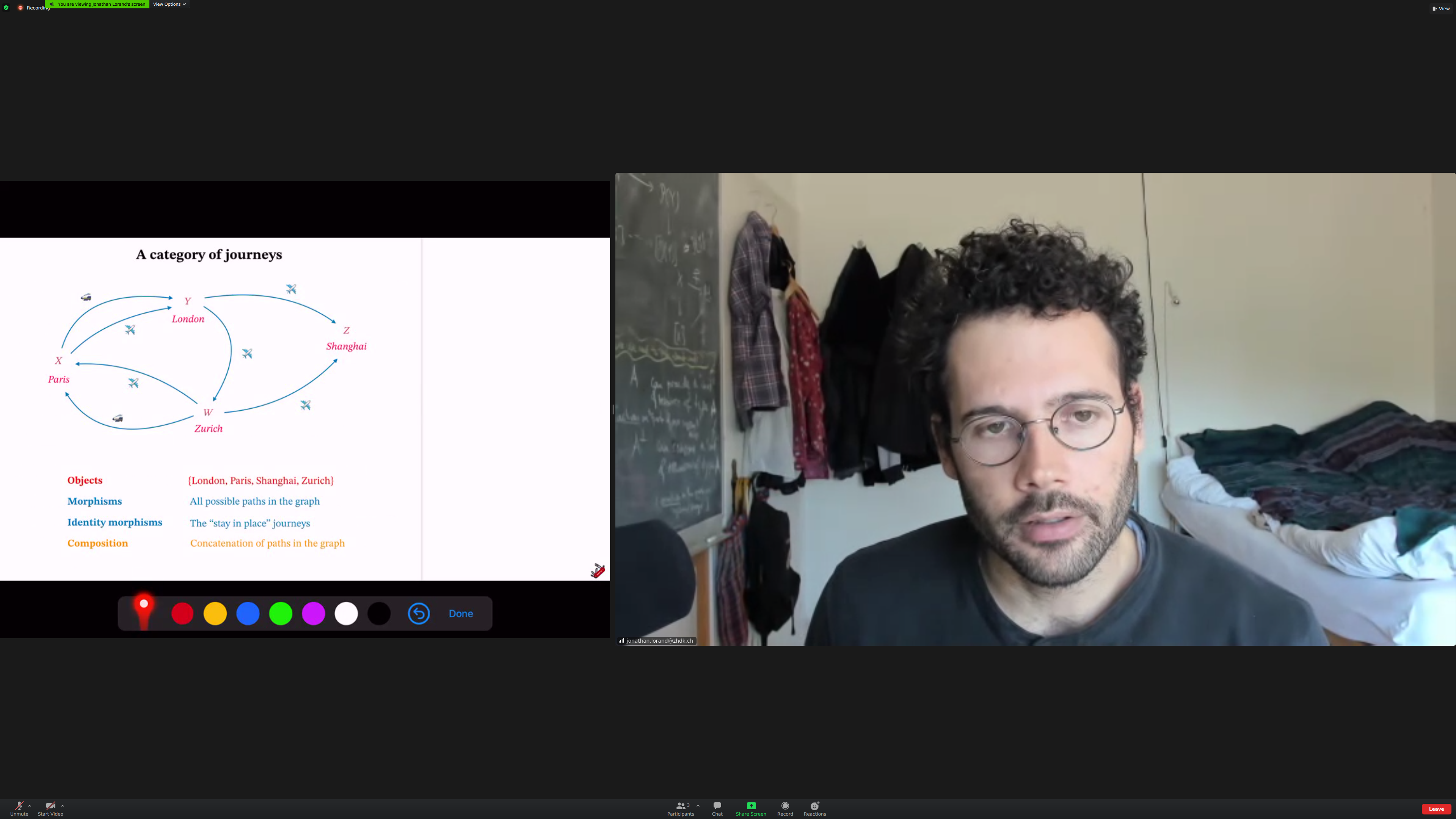
Example: composing [[journeys]].
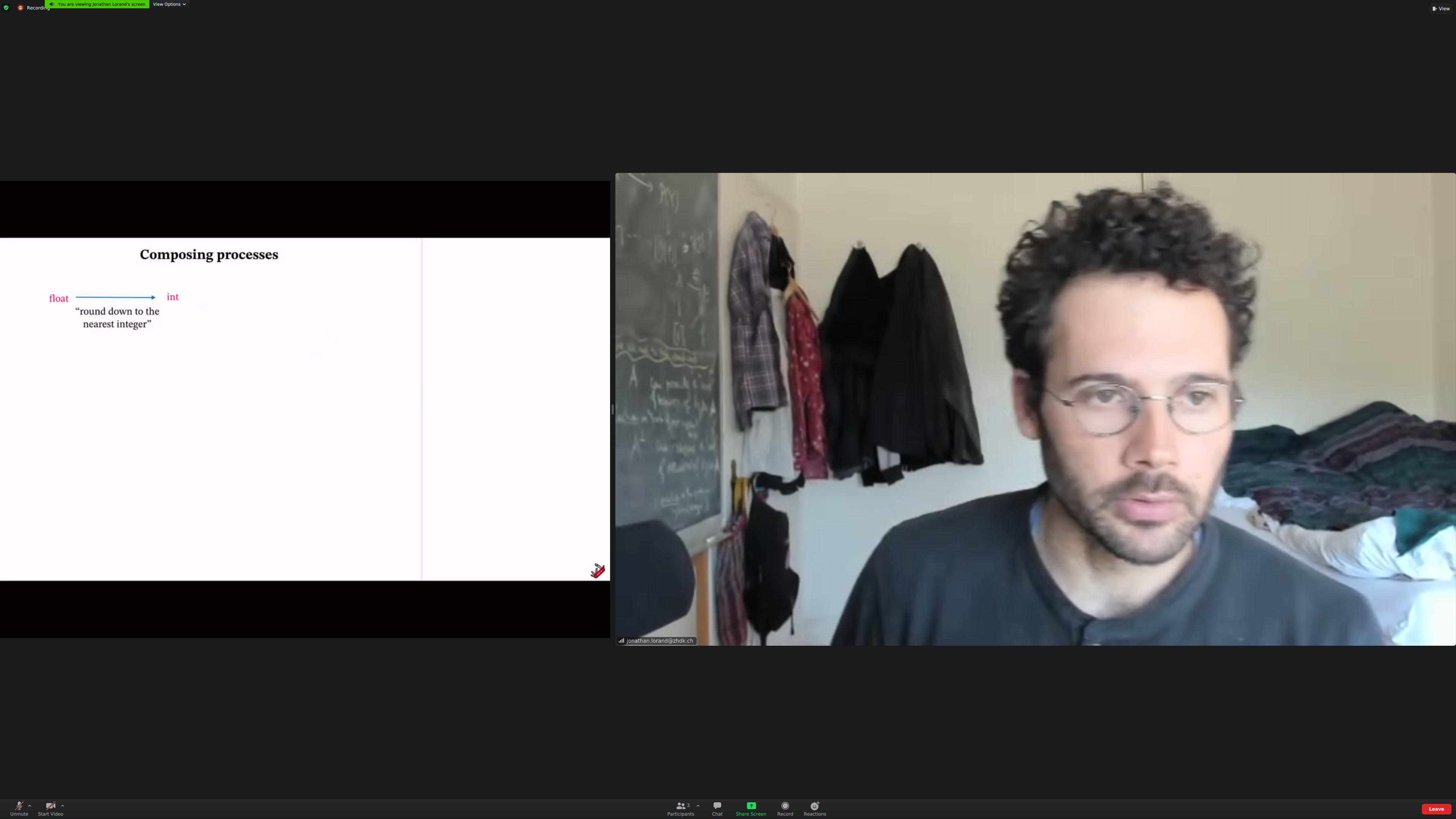
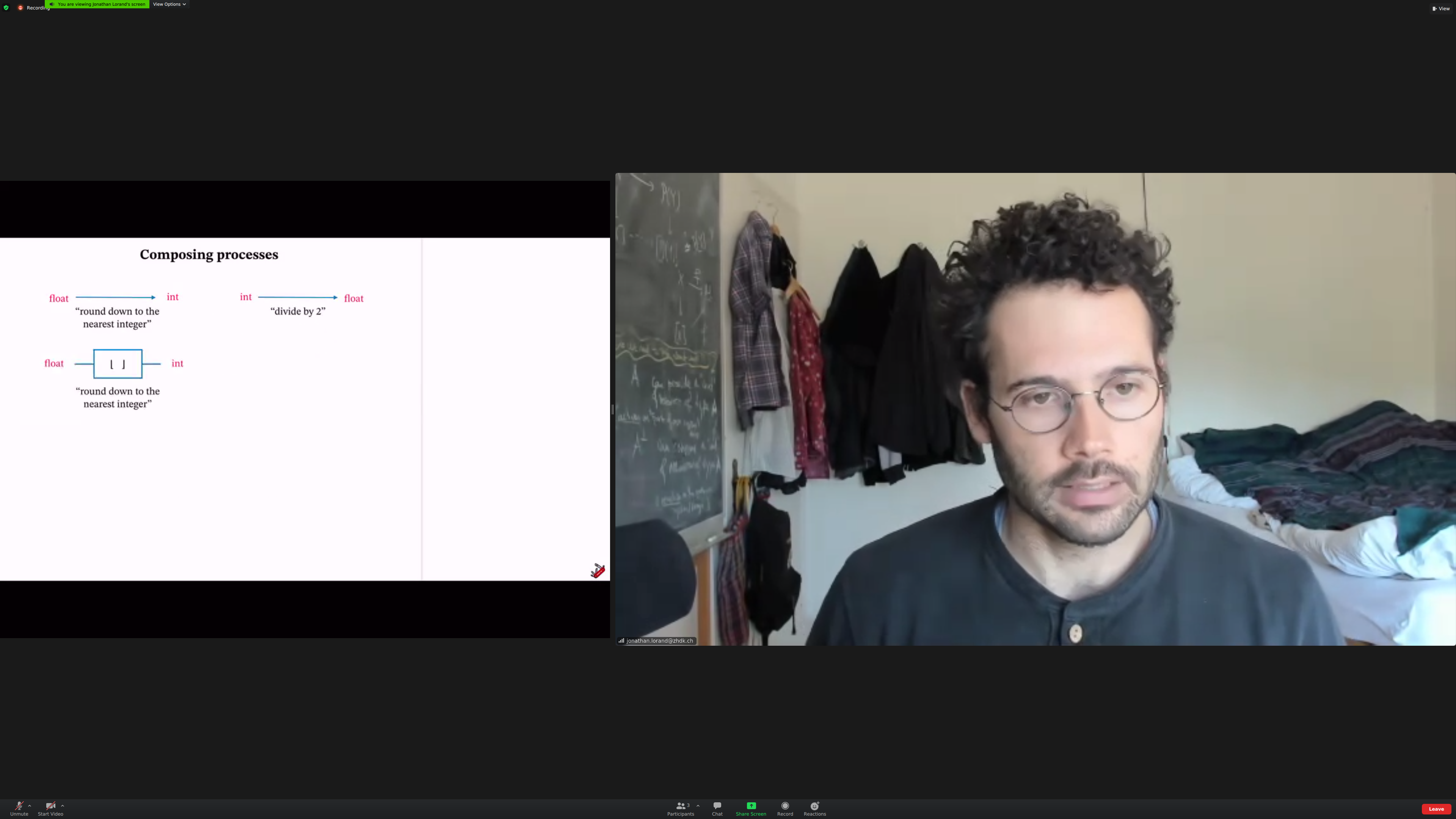
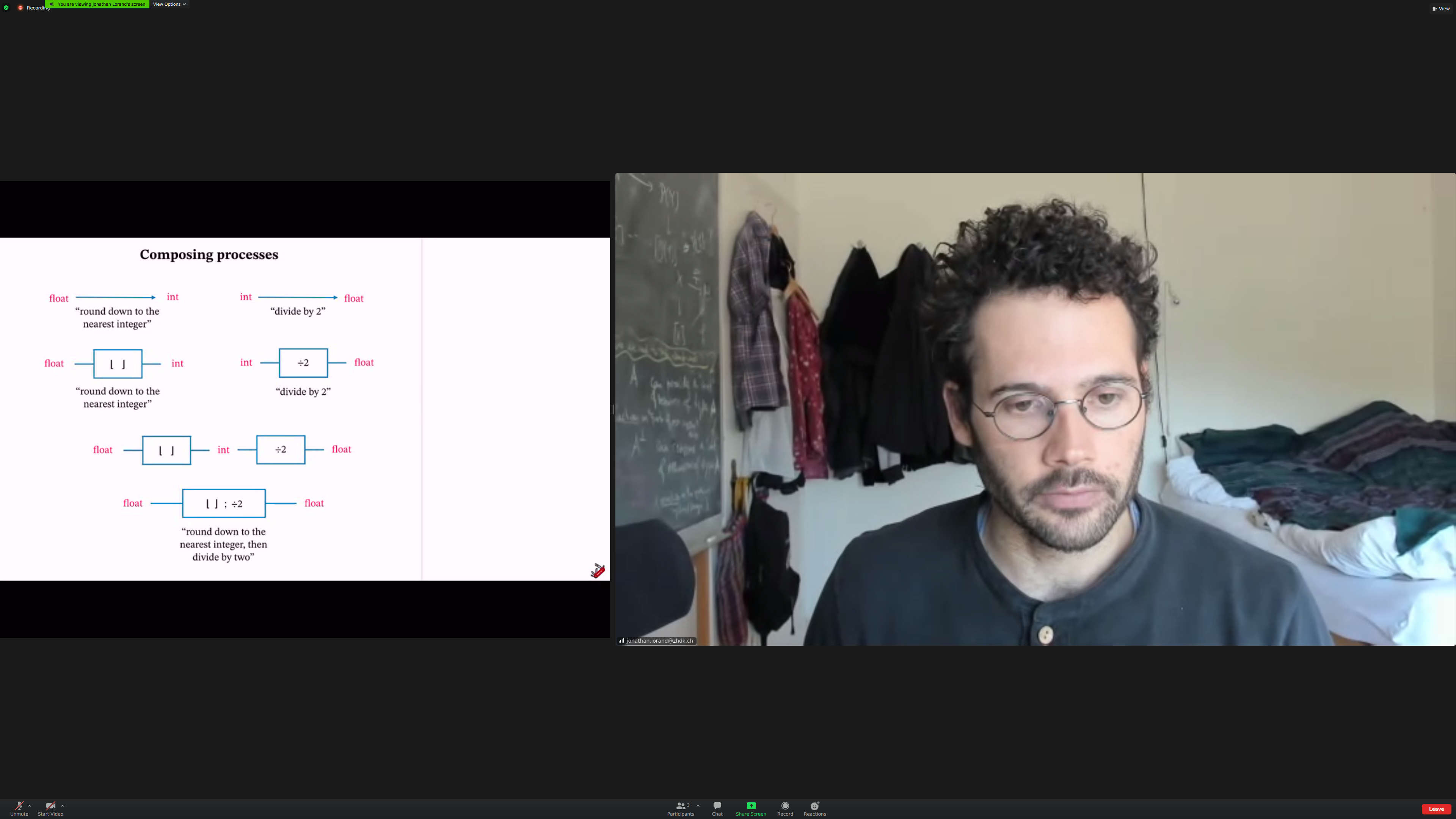
Example: composing processes. Mathematical functions, algorithms, physical processes.
Notation: boxes instead of arrows. Directionality is from left to right.
The output of the first box is the same [[type]] as the input of the second.
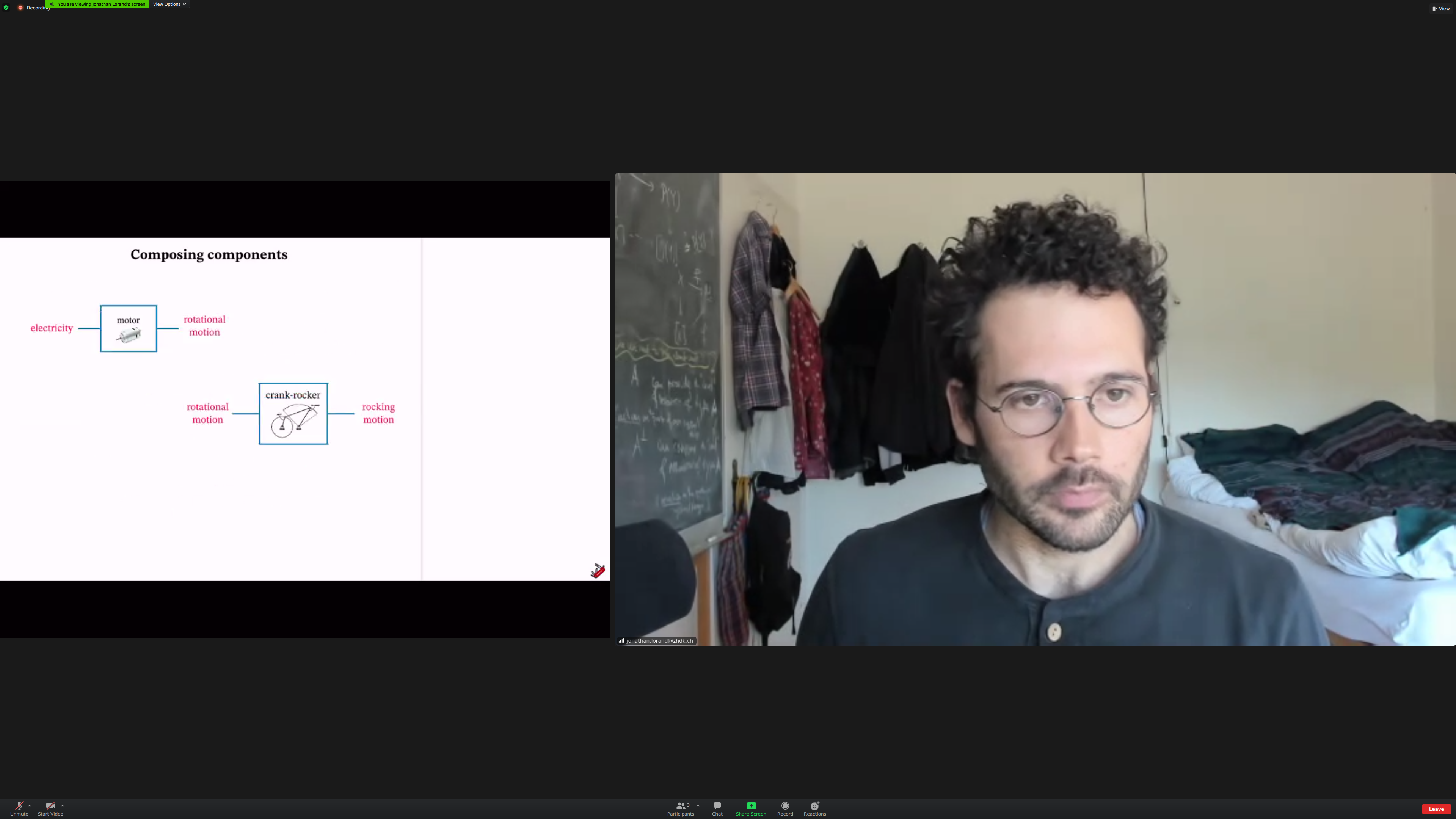
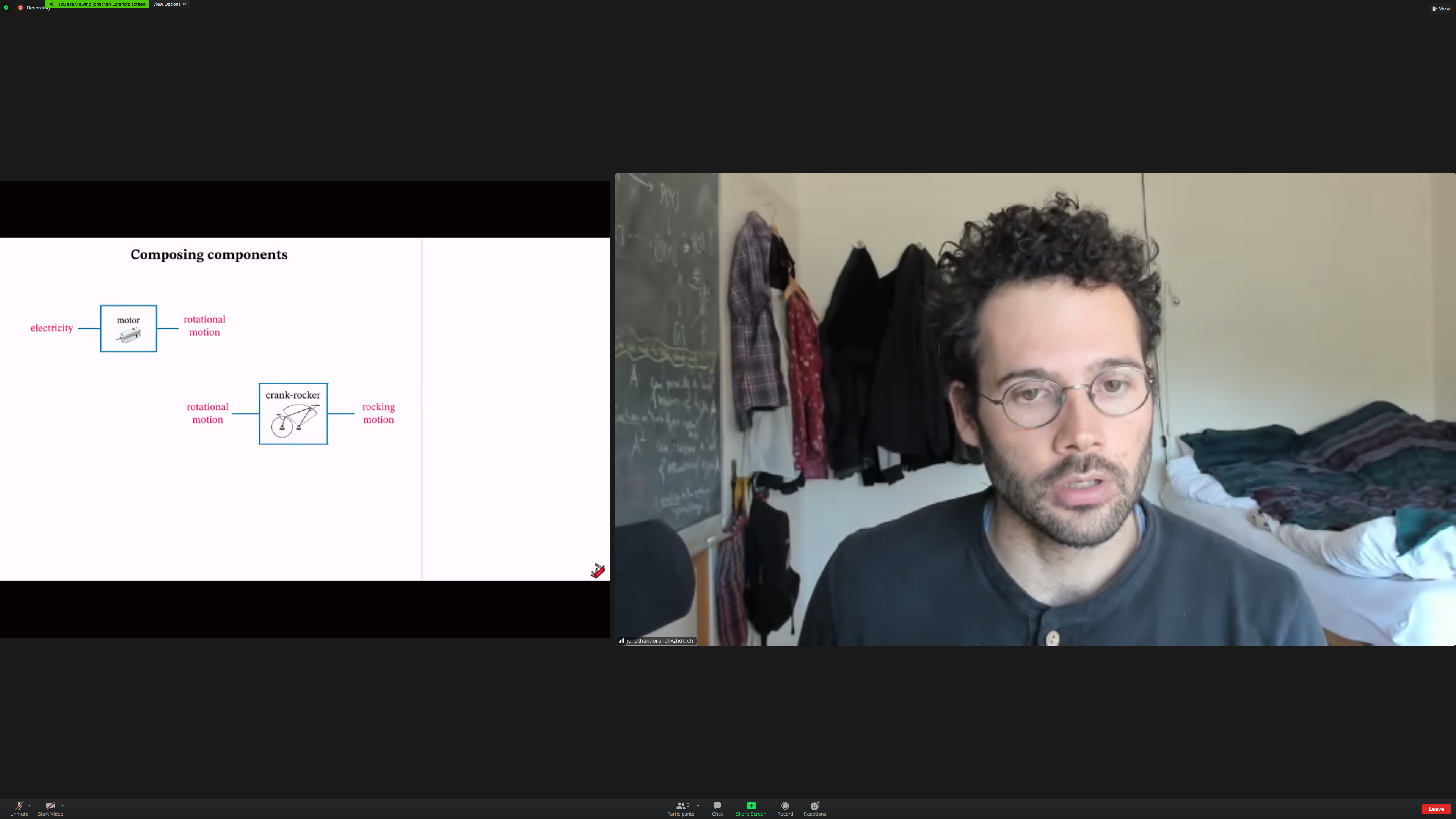
You can also compose physical components, of course.
And physical processes.
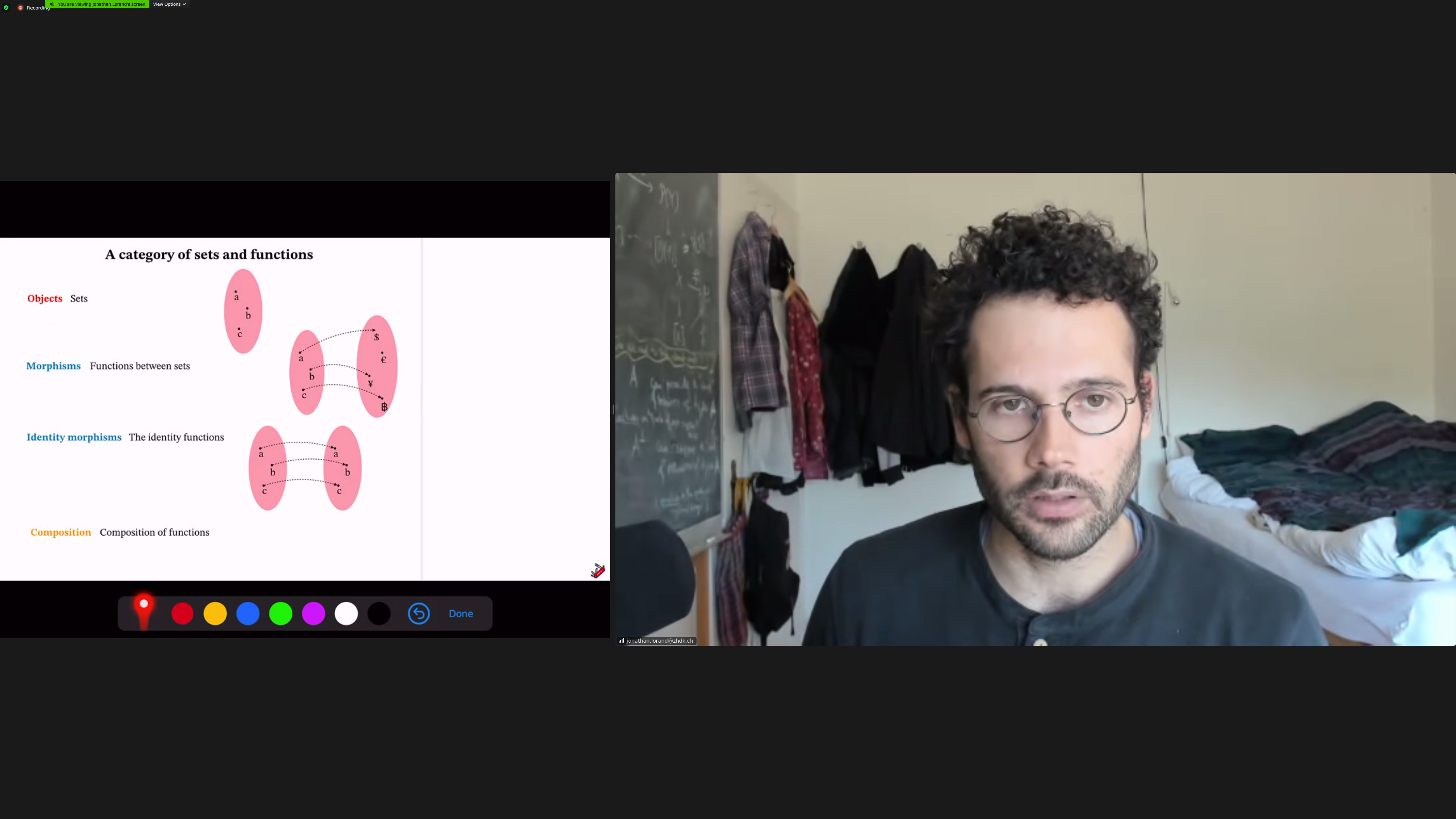
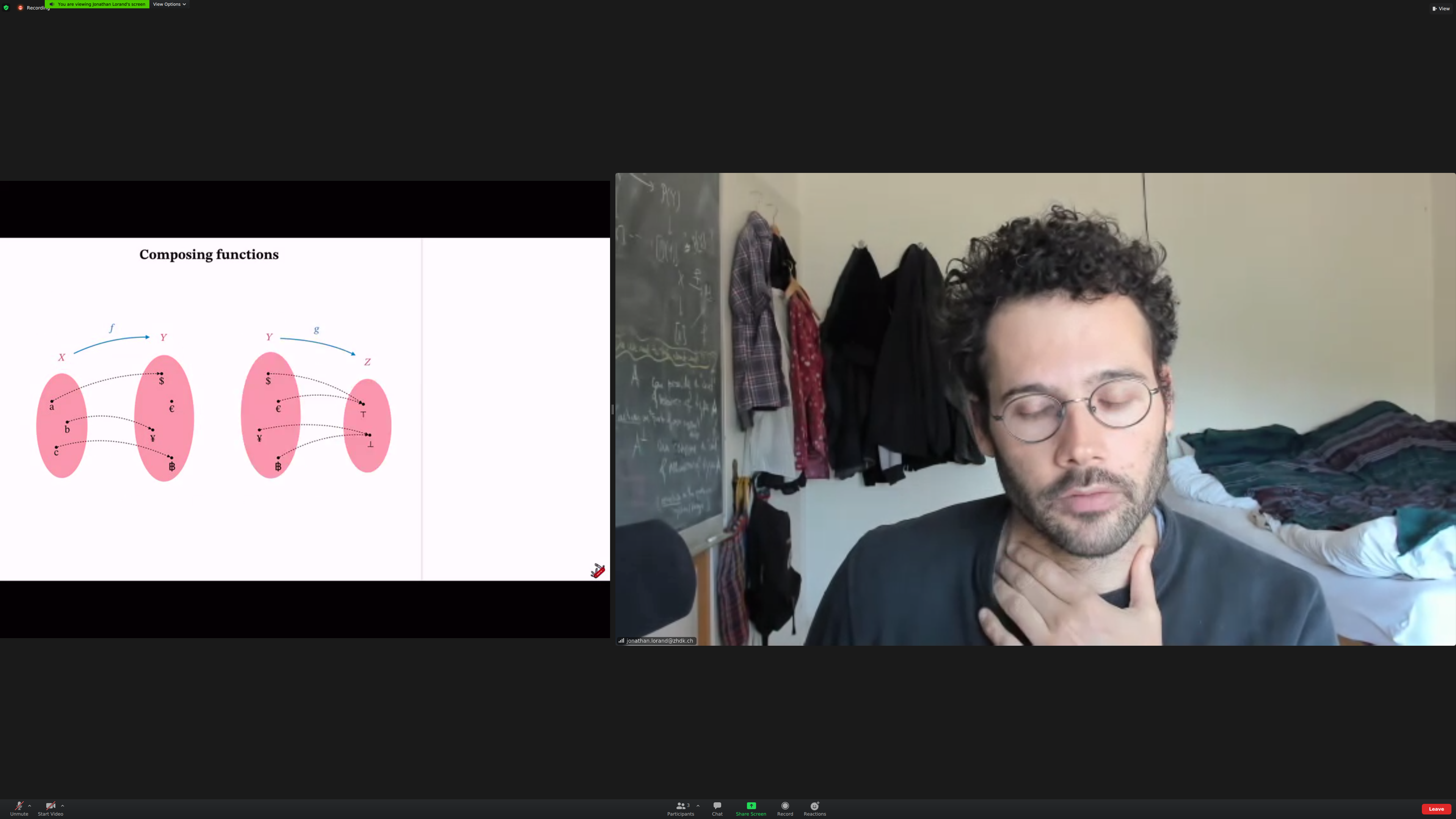
The fundamental example is mathematical; composing functions as sets.
Aside: we should put this on youtube.
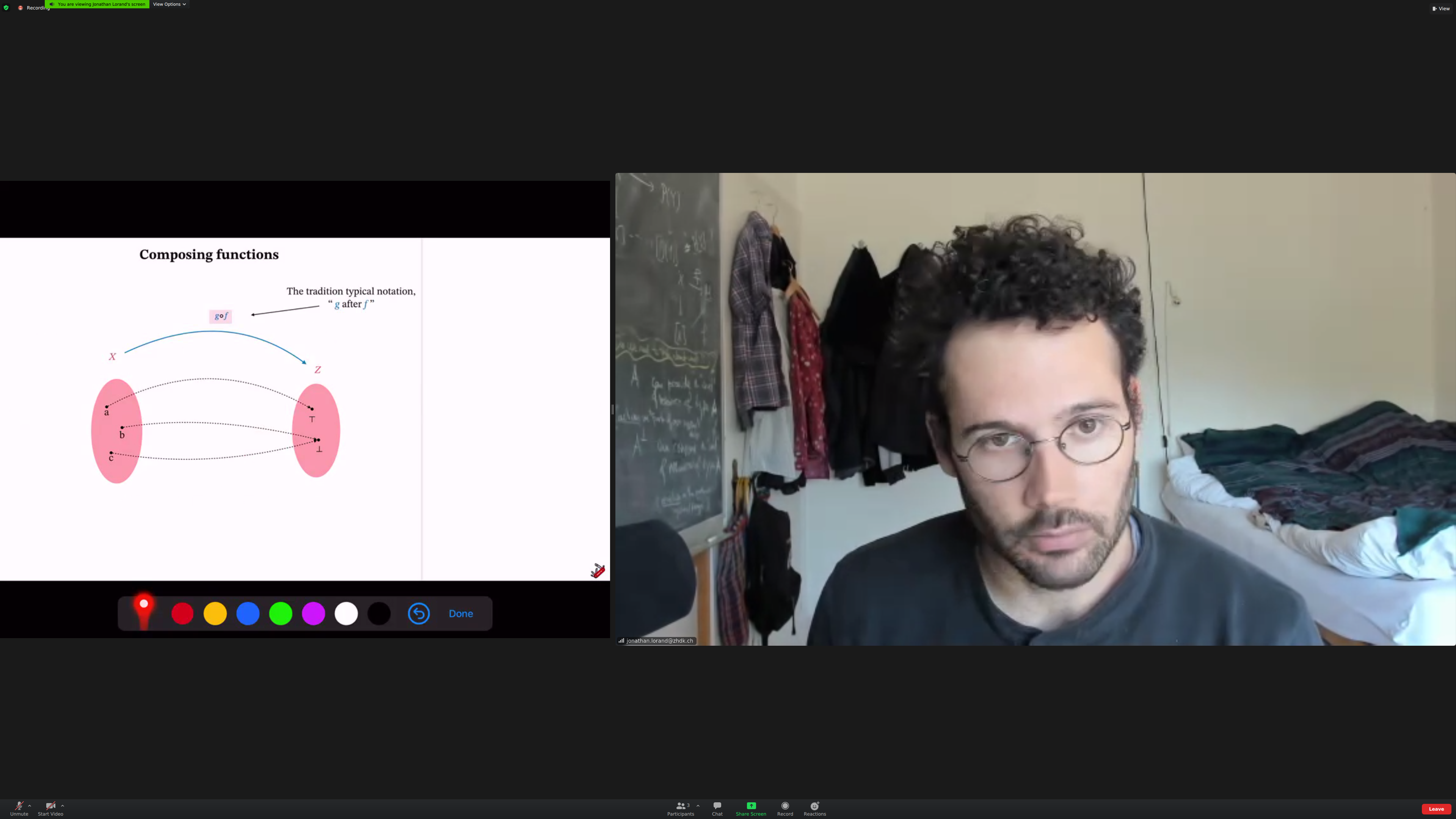
We'll be used 'then' notations for compositions, not traditional.
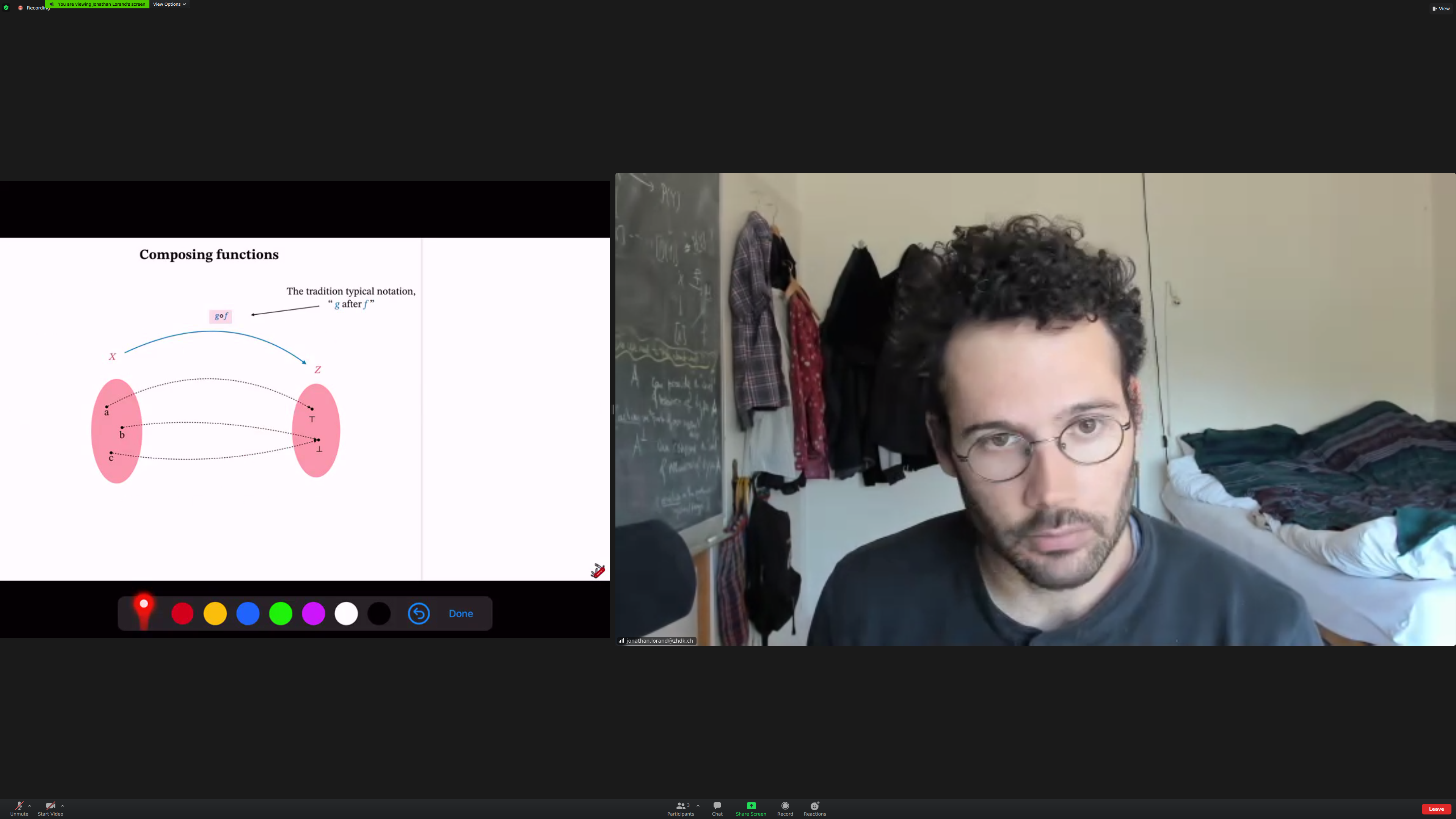
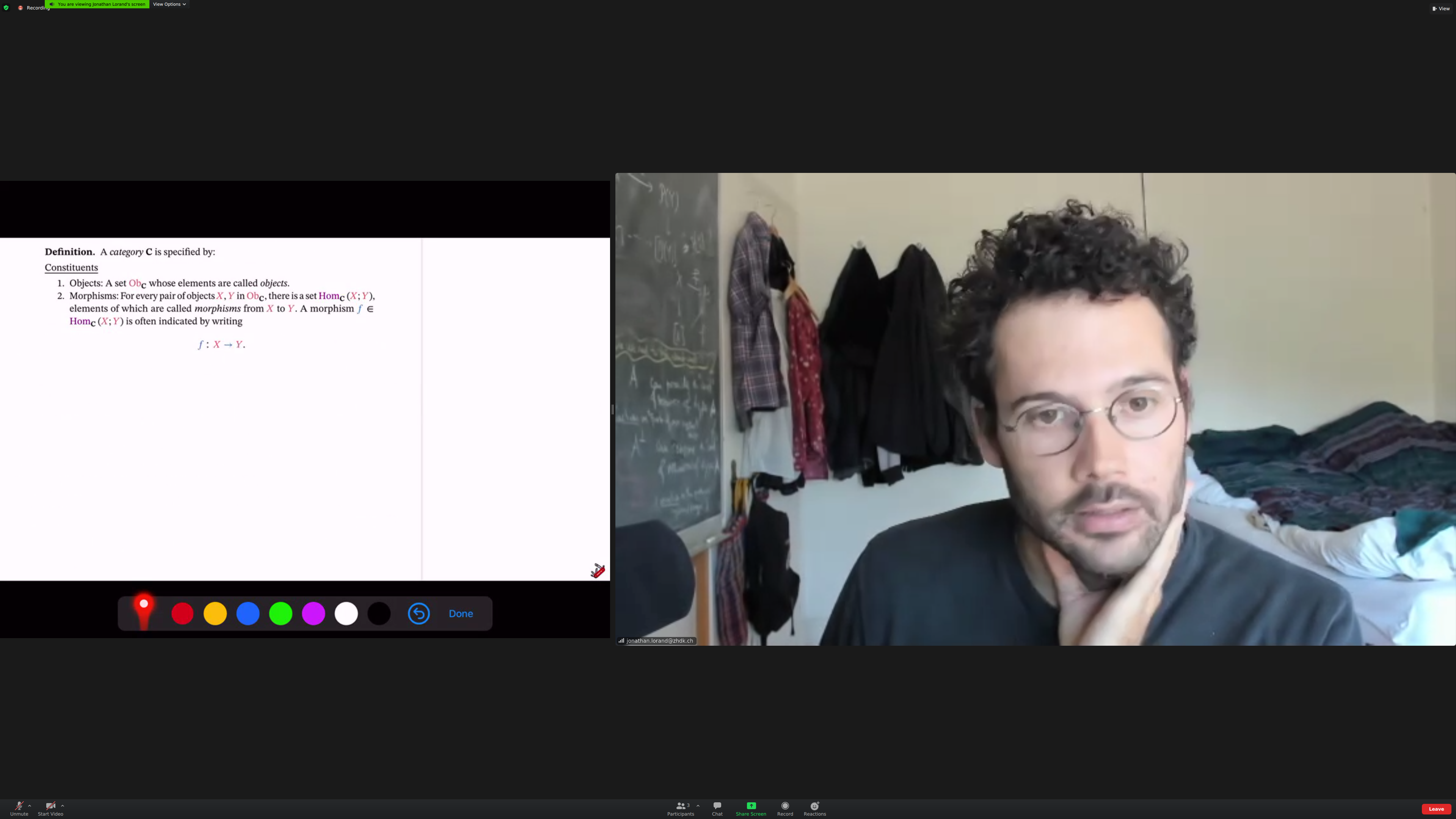
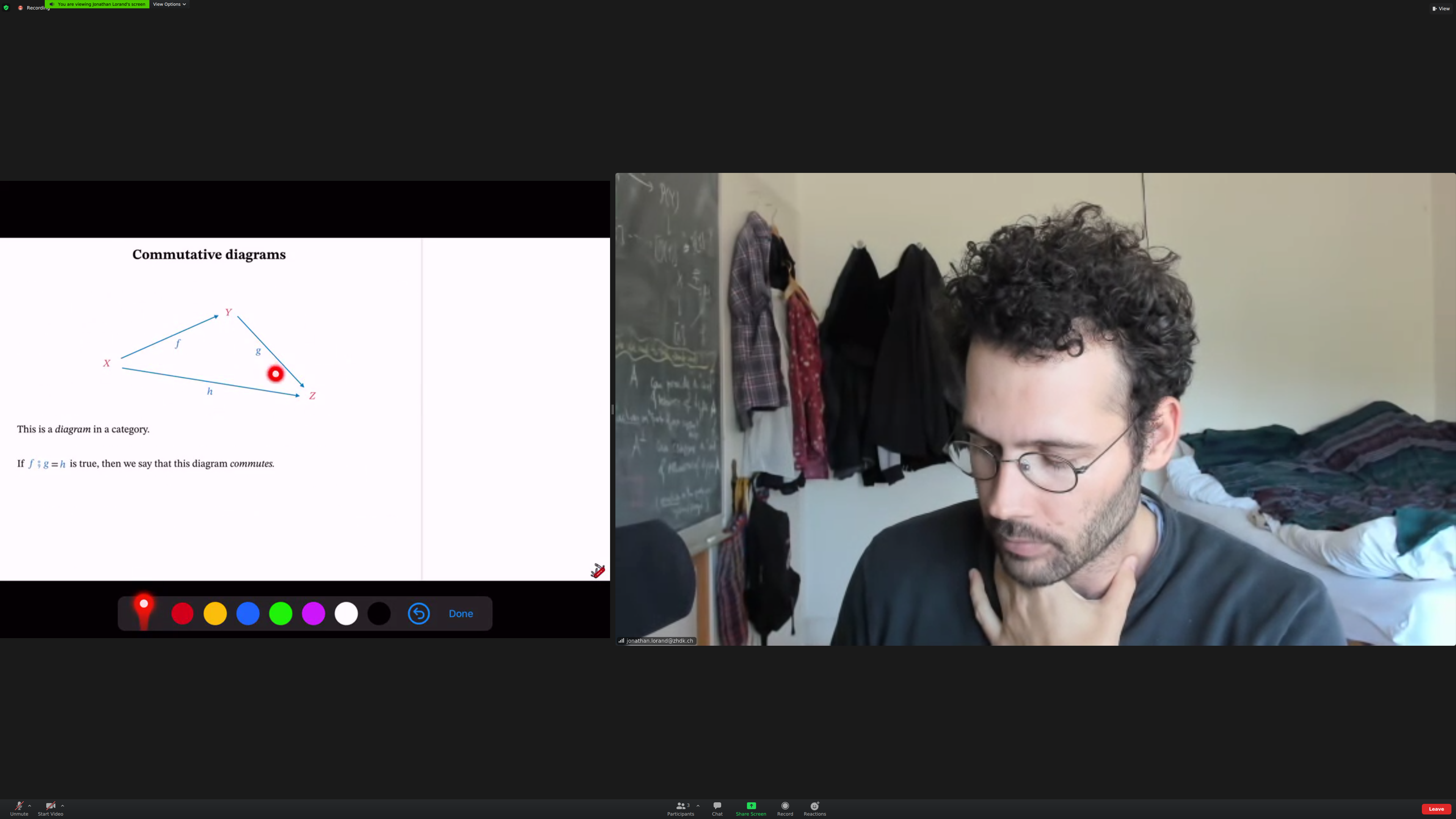
We'll relate [[objects]]. The things doing the relating are [[morphisms]].
(here there should be a better screenshot, I couldn't get it on time)
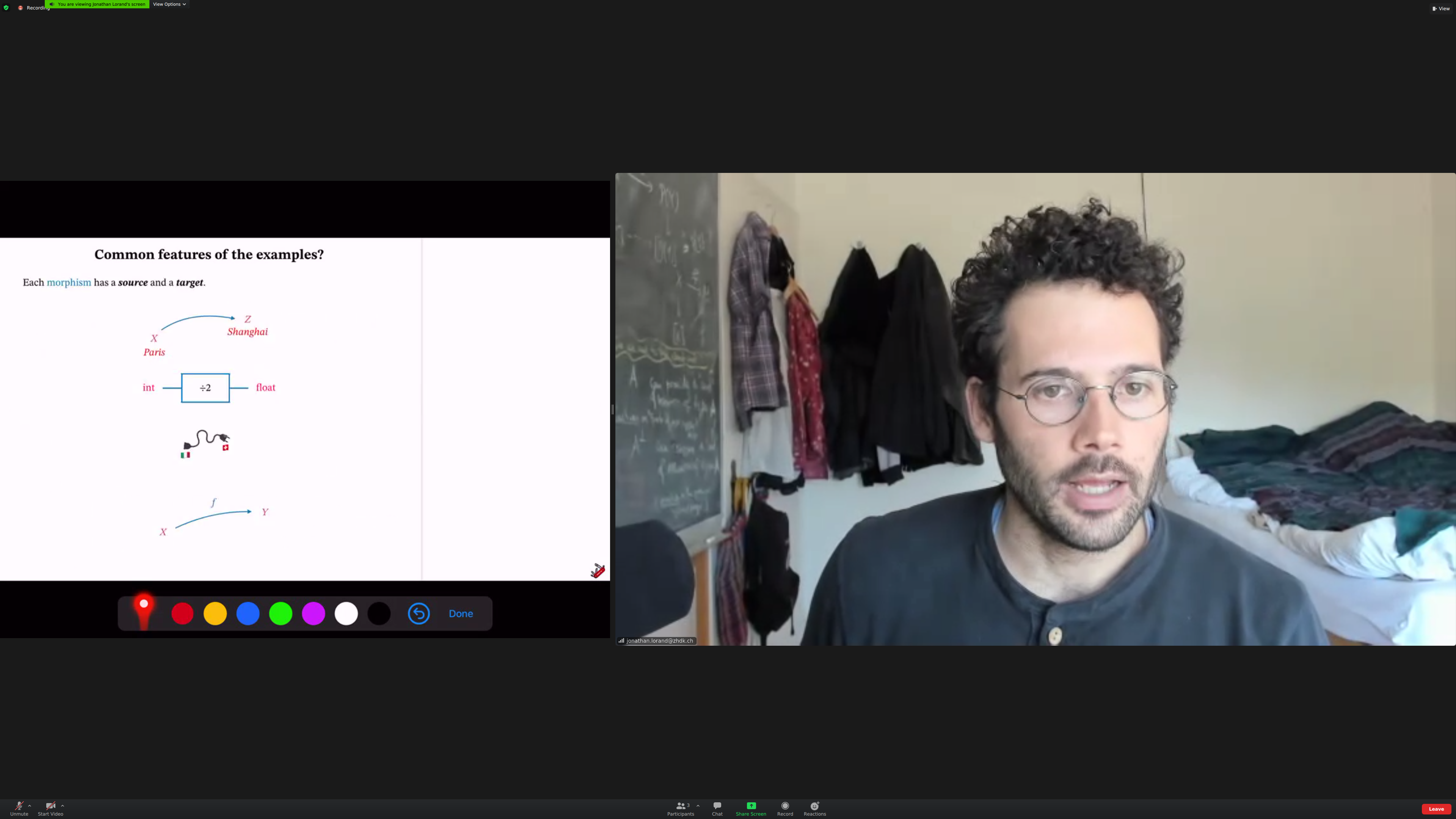
Each morphism has a [[source]] and a [[target]].
We can compose morphisms when the target of the first matches the source of the second.
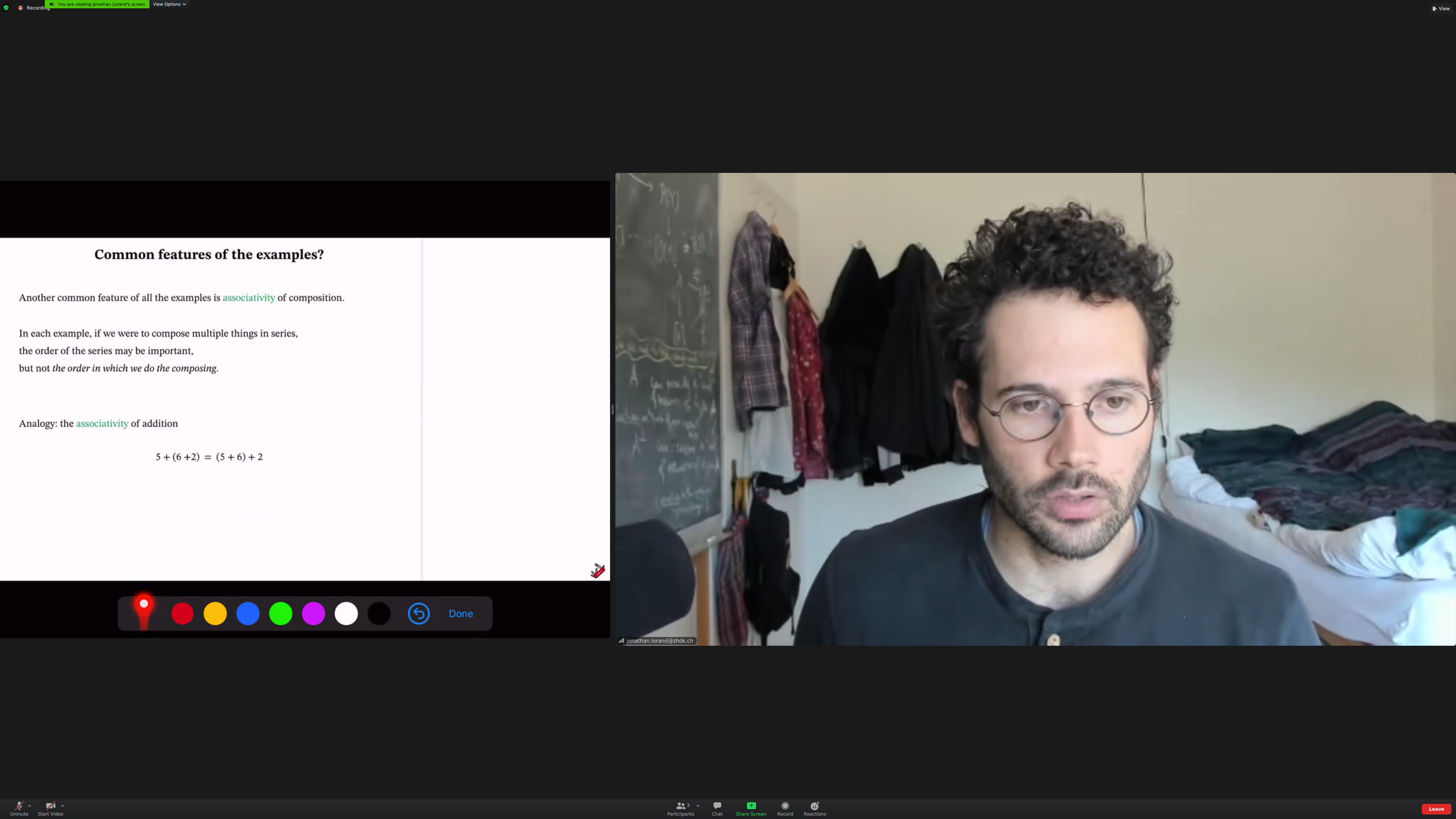
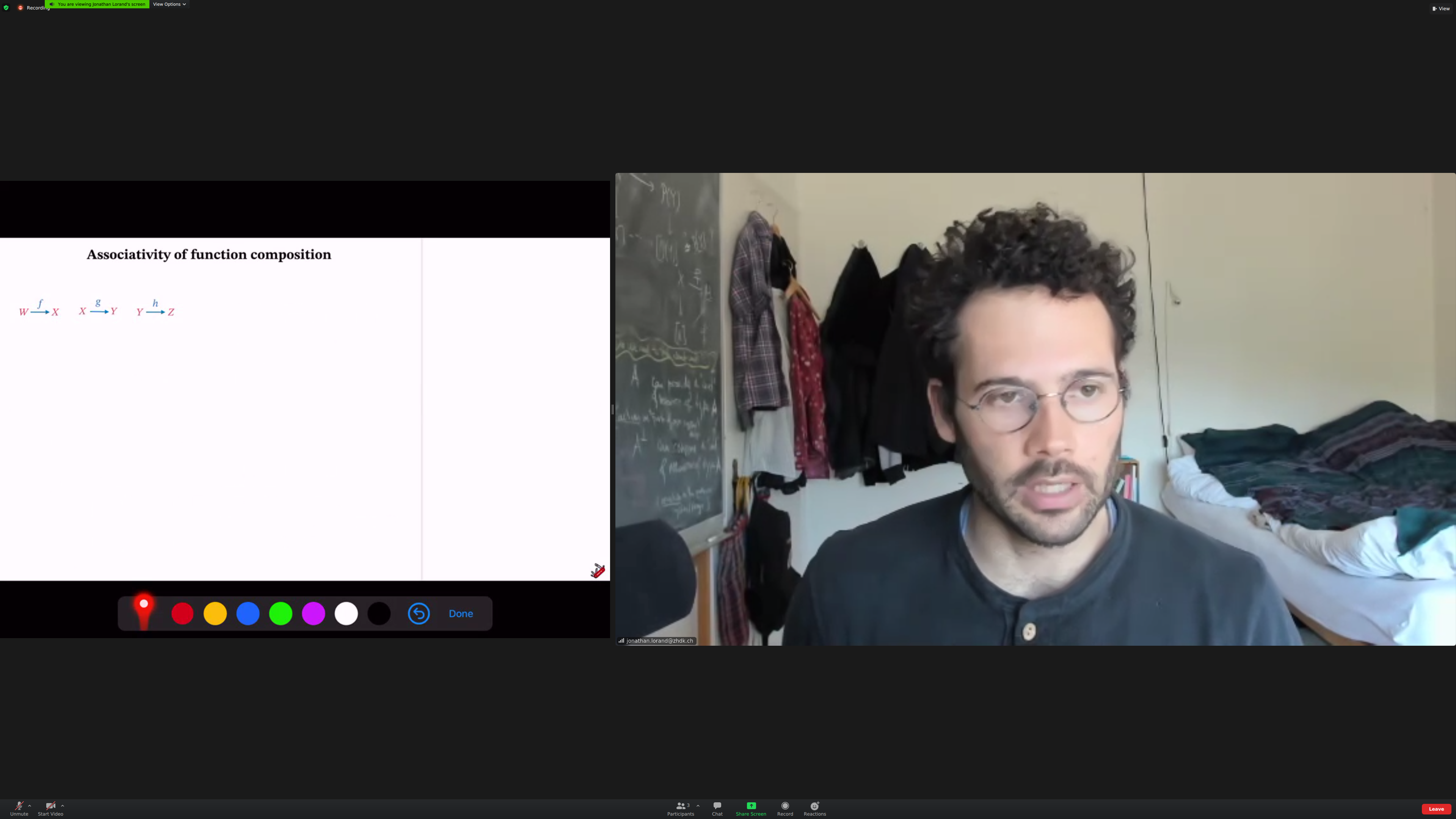
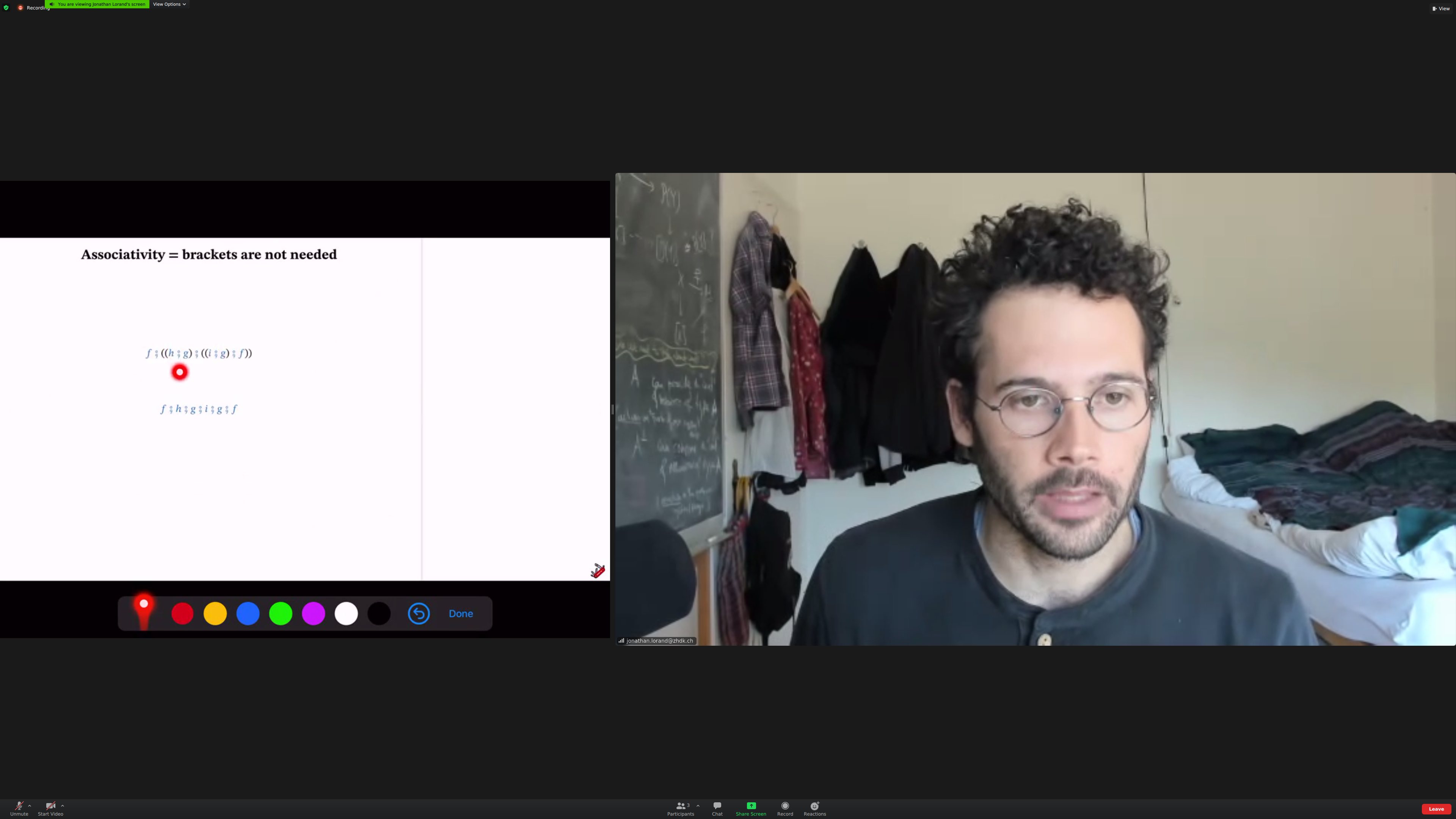
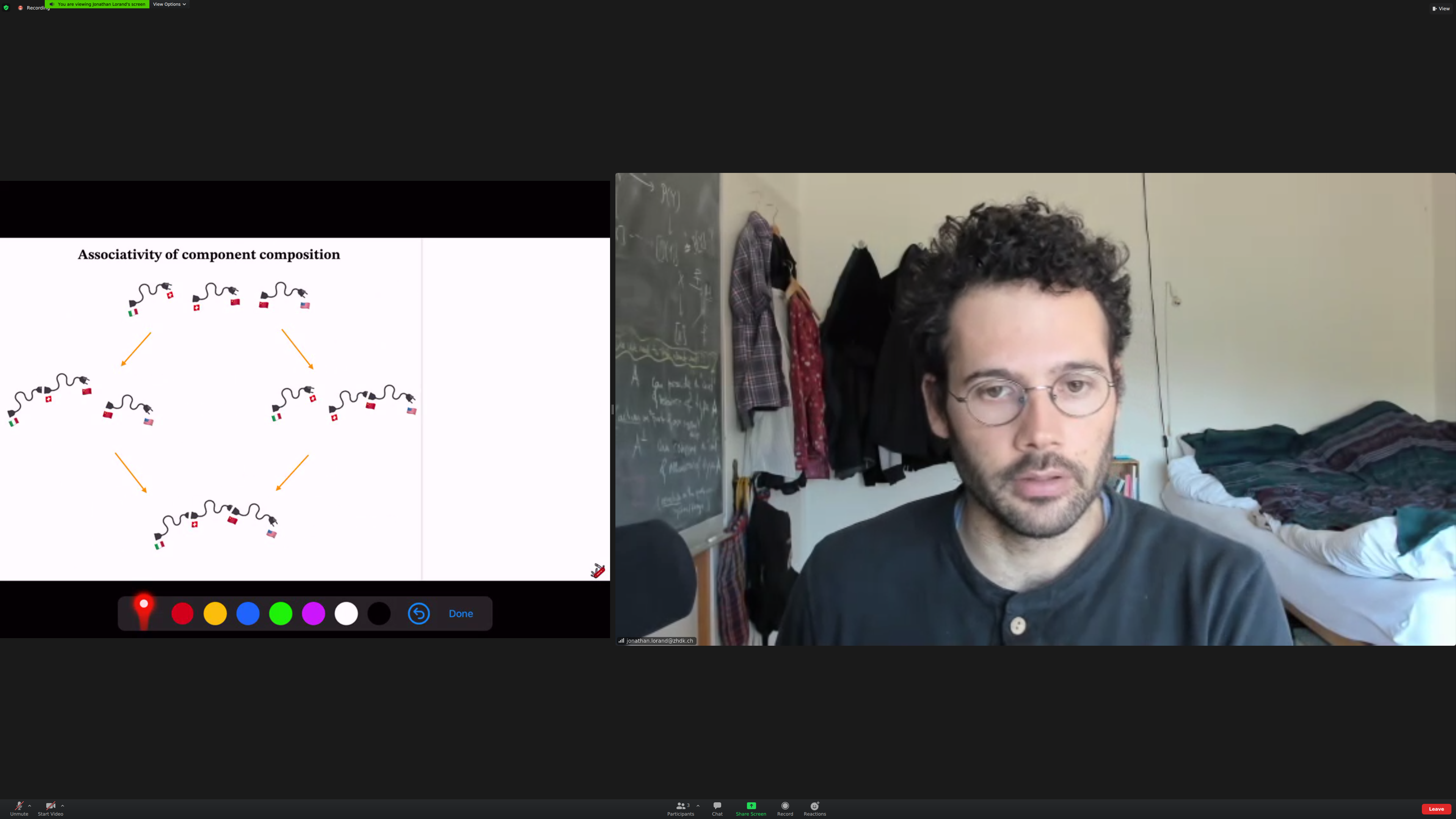
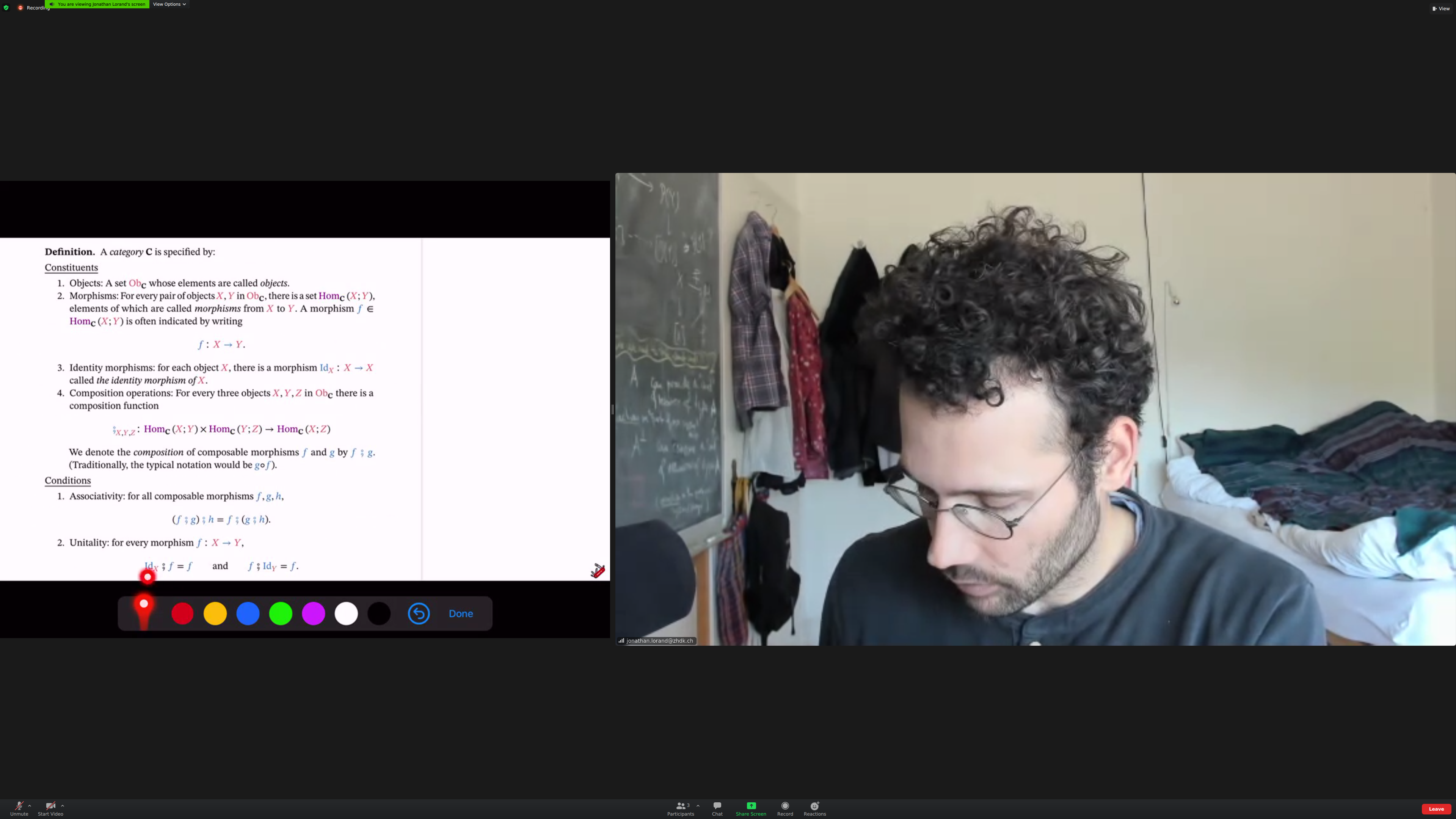
Common feature of all examples: they are [[associative]]. The order of composition doesn't matter; the order of application may. (check)
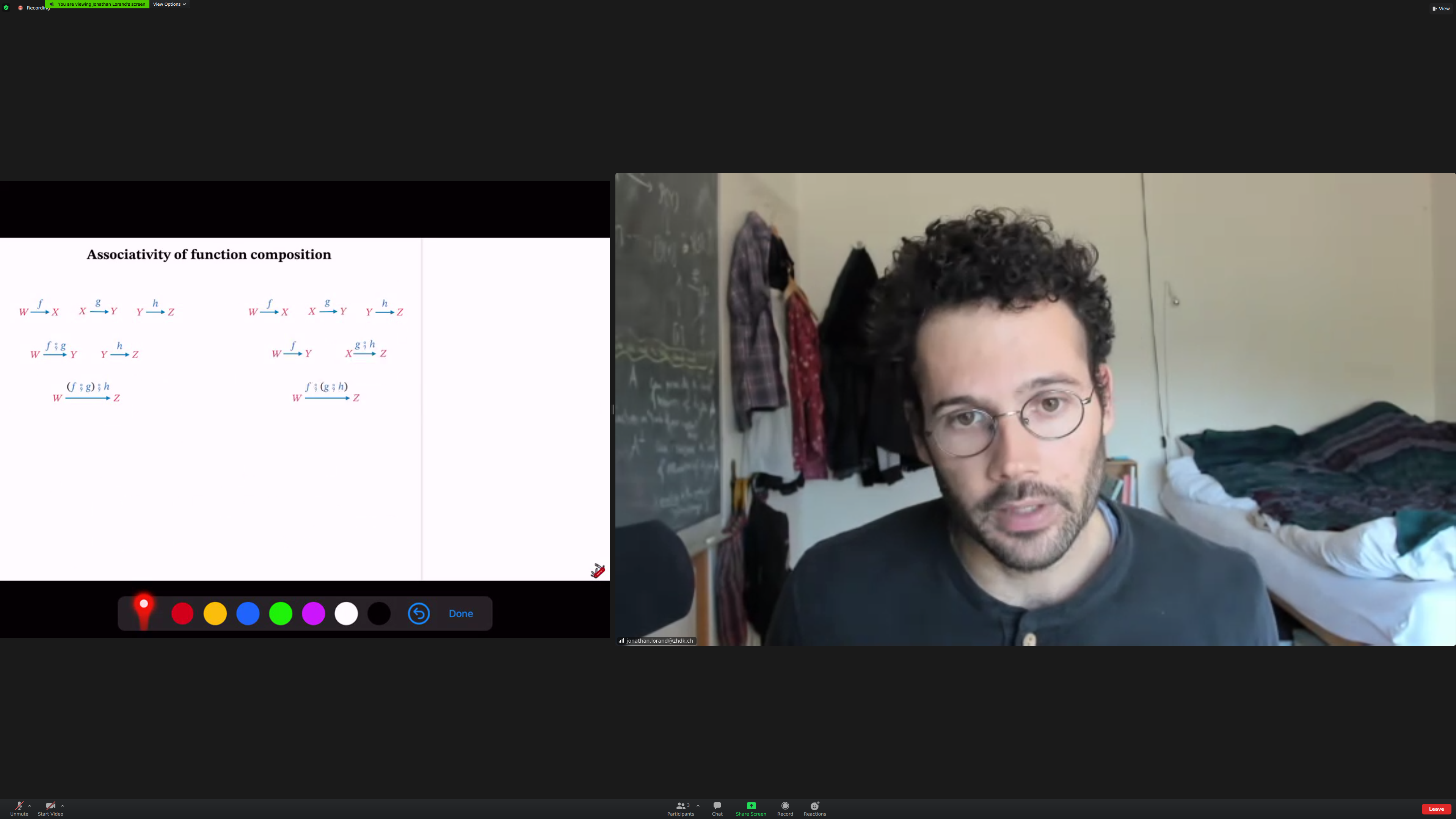
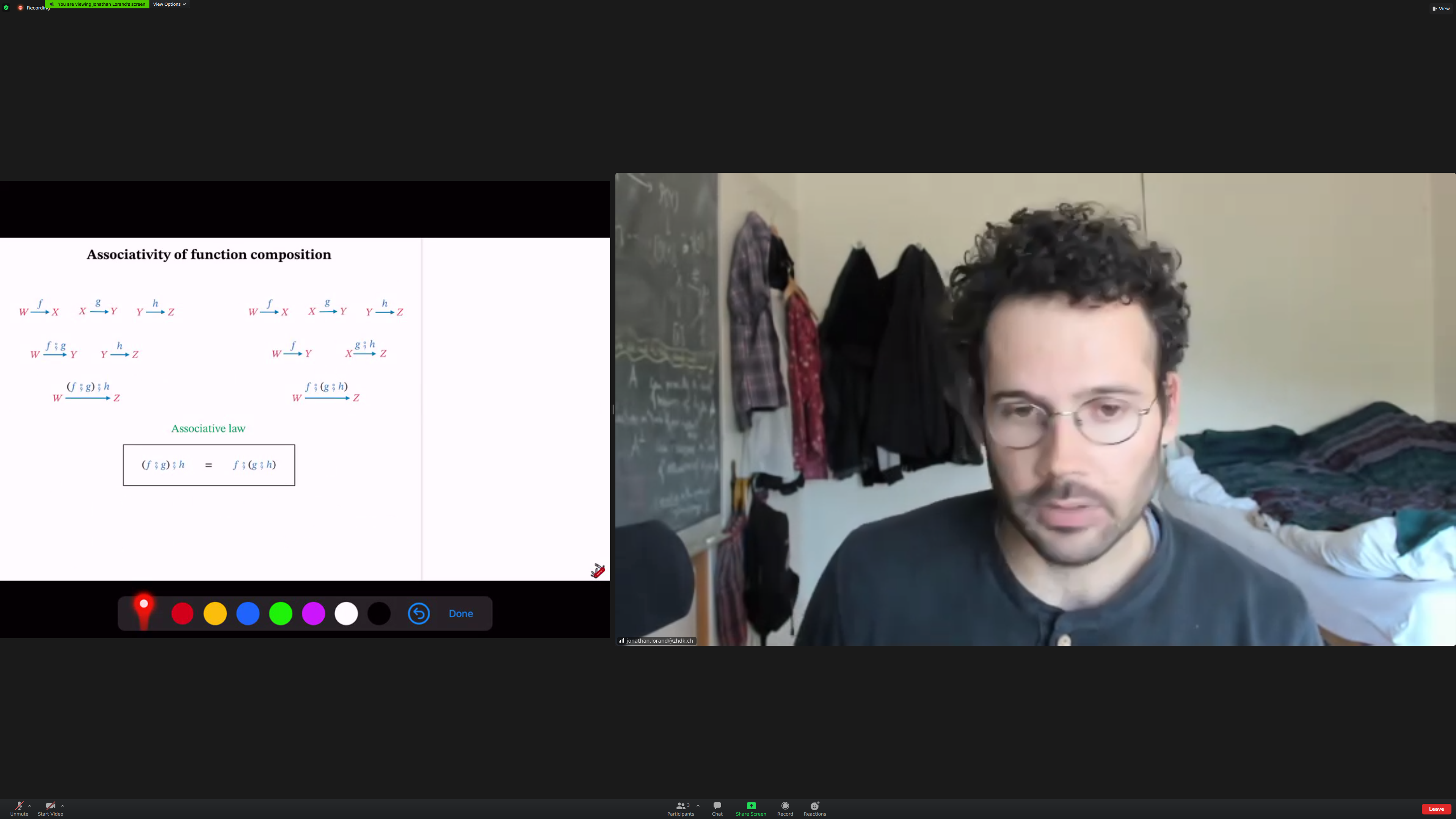
This was [[true]] for all the examples we looked at so far.
Associativity means that brackets are not needed.
Aside: going from a class in real time to screenshots is one morphism; going from screenshots to notes is another. Going from notes to a chapter or blog post is another.
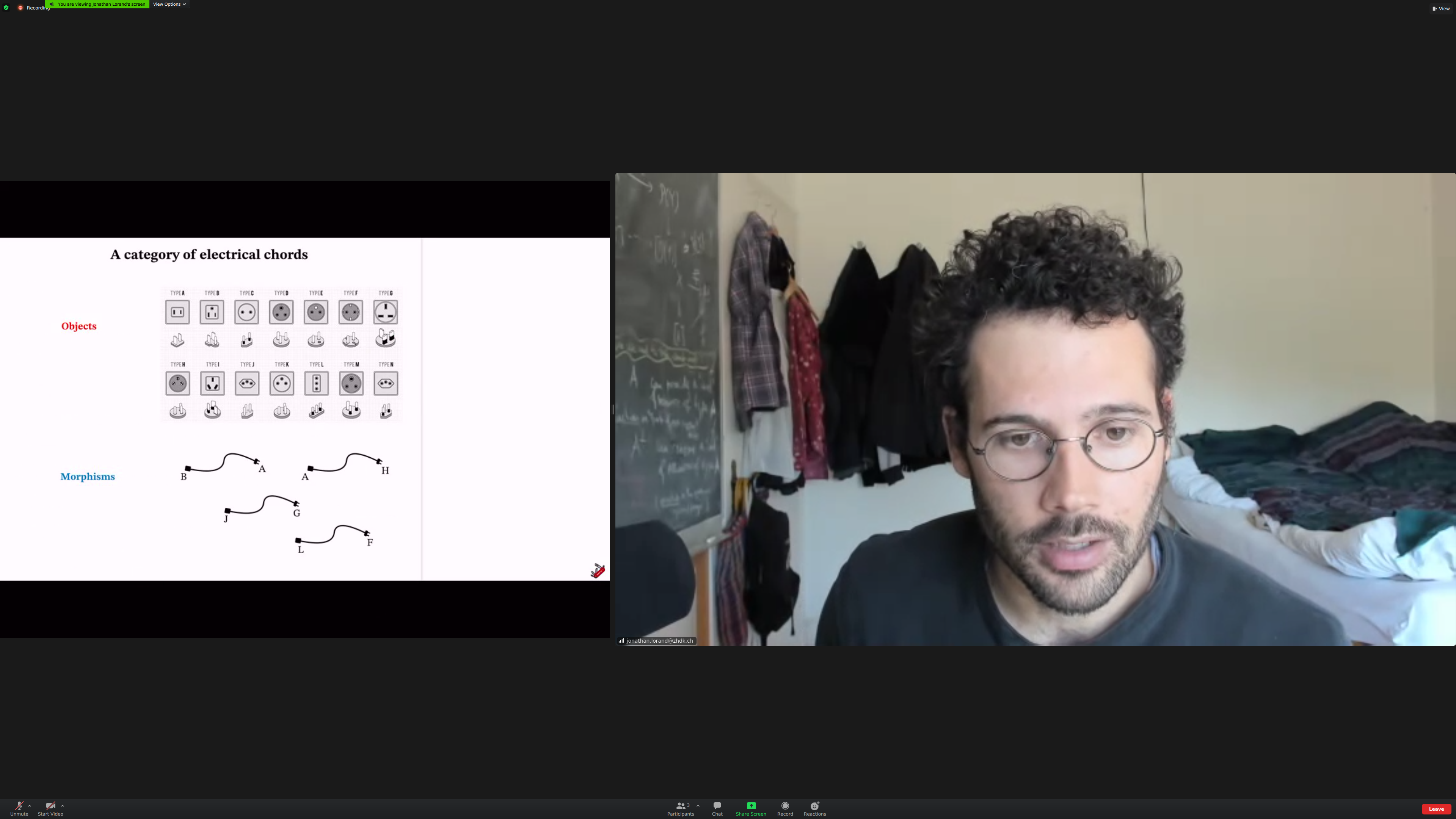
Associativiy in plugs:
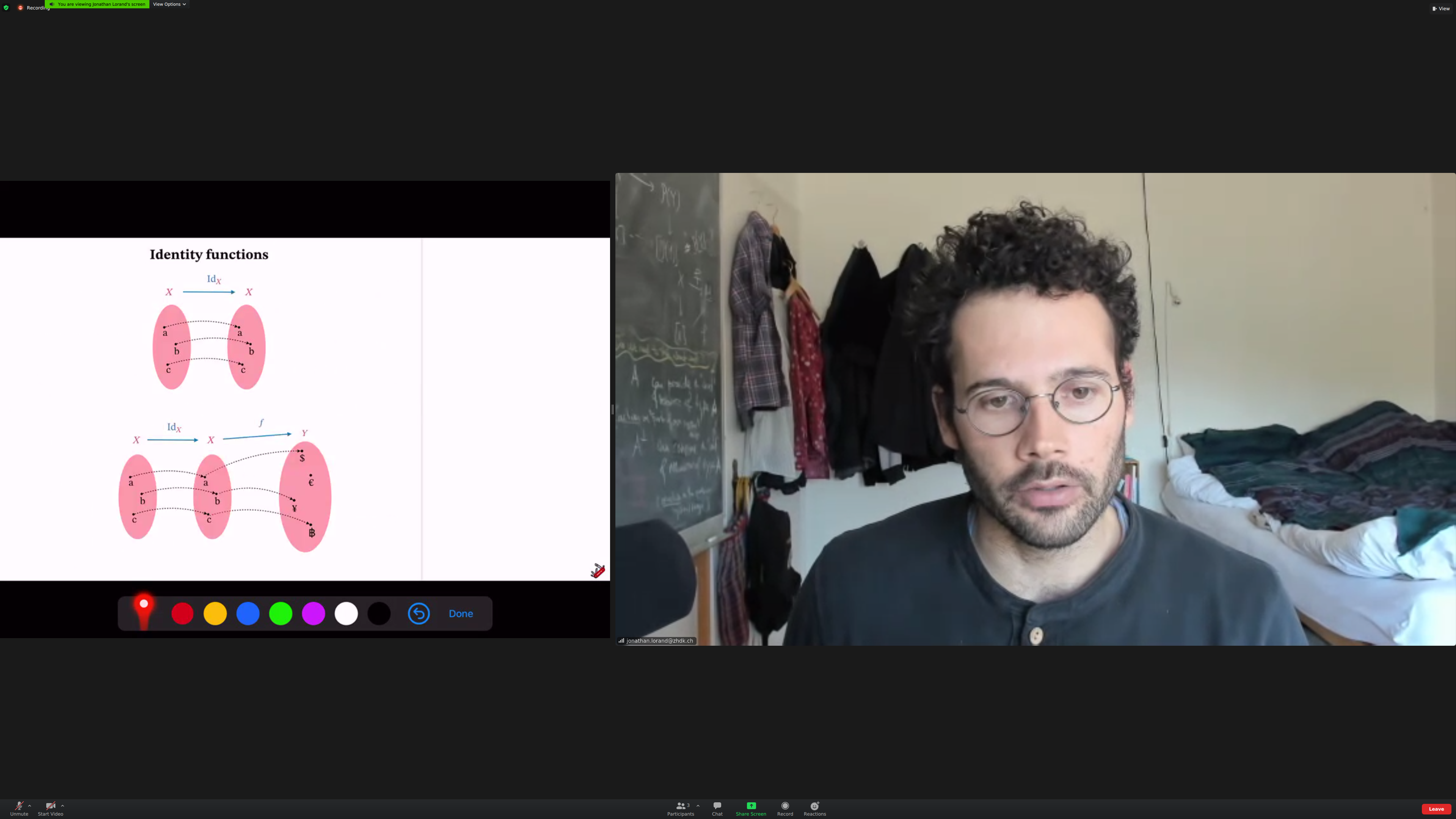
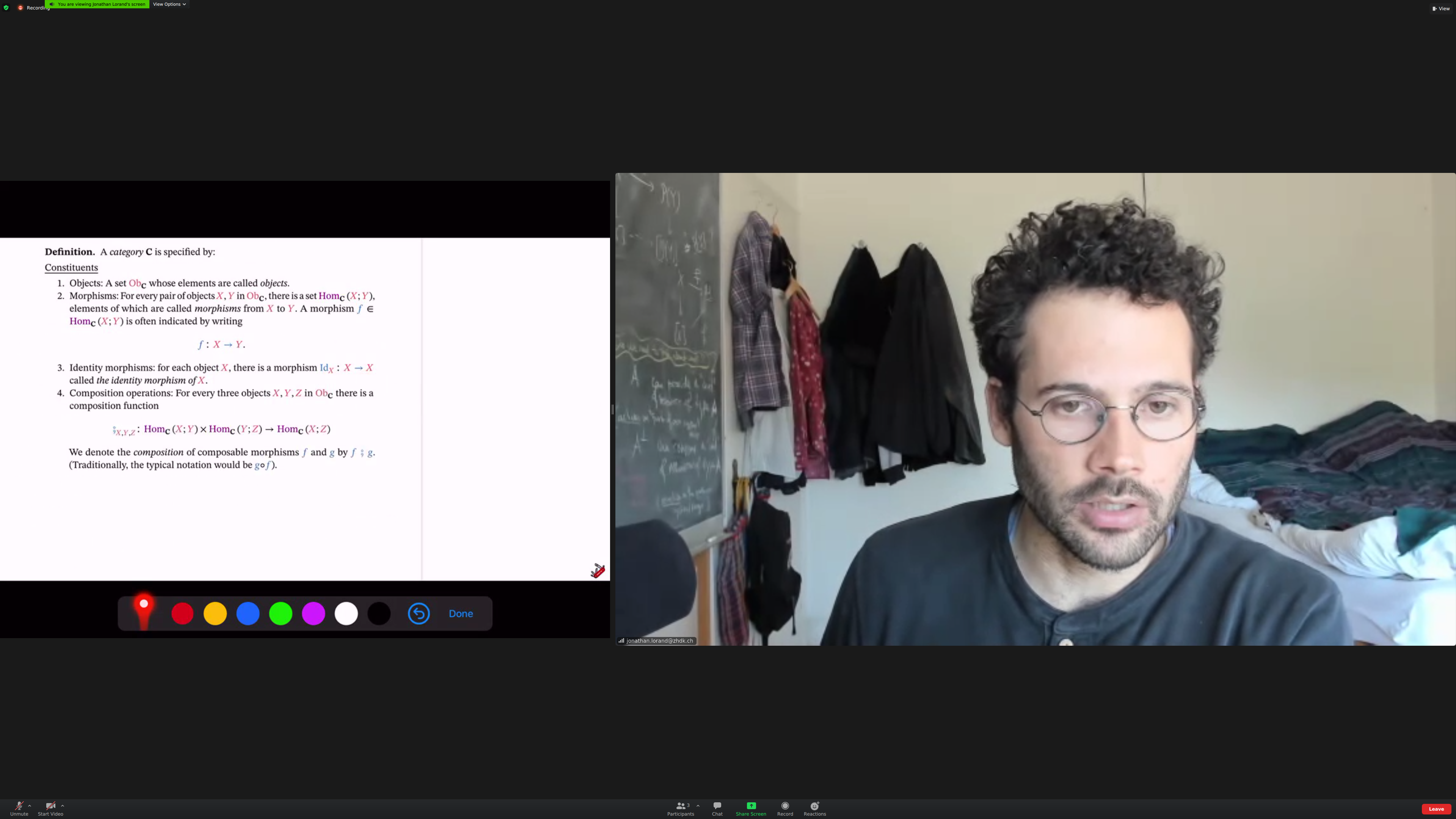
Identity morphisms: morphisms that do nothing. Like a zero in addition.
Identity morphism for functions: the identity function.
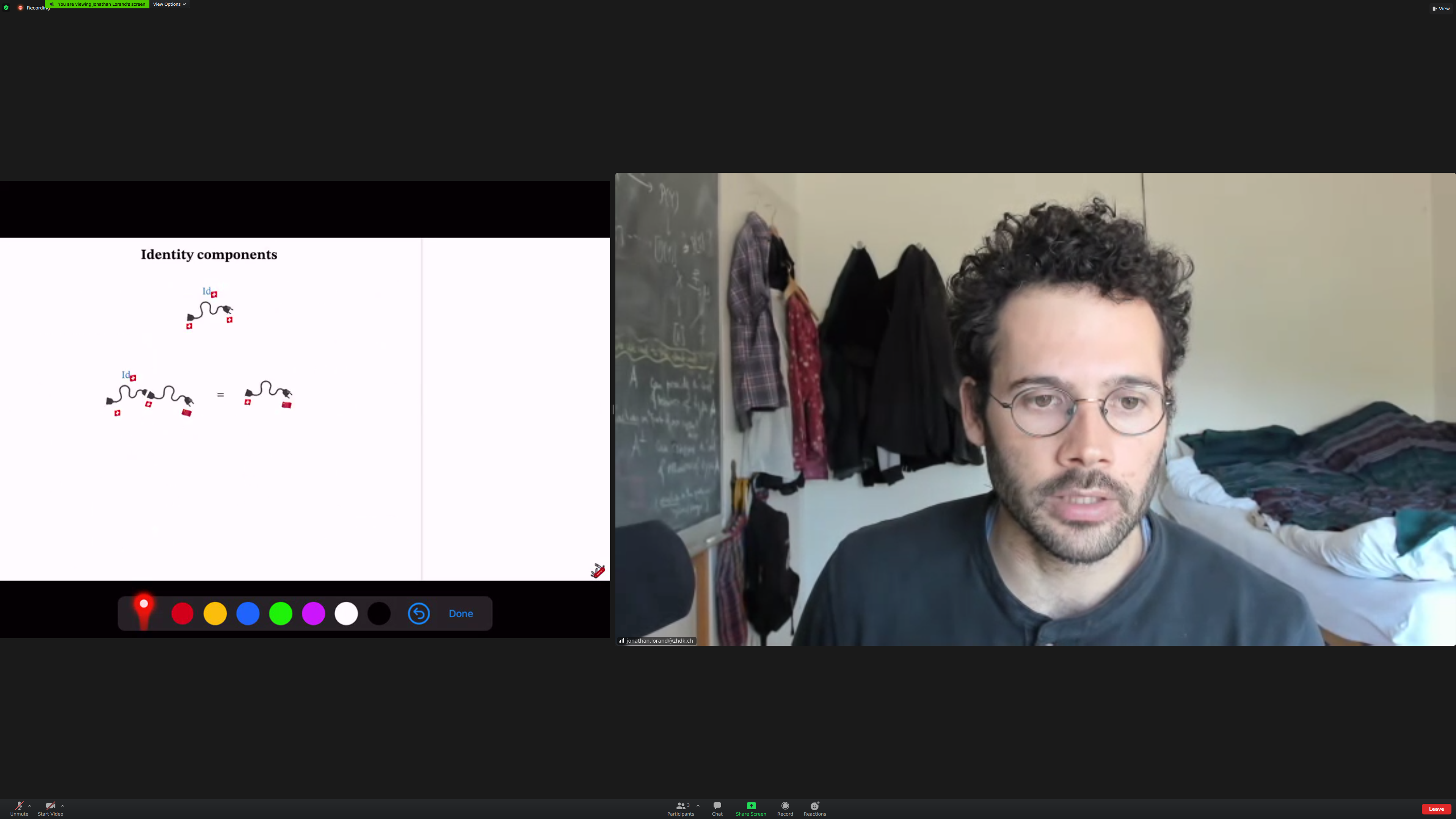
A converter that converts to the same electrical standard is just an extension that can become a converter of any type with one additional composition.
[[identity journeys]] (aside: I call these [[excursions]])
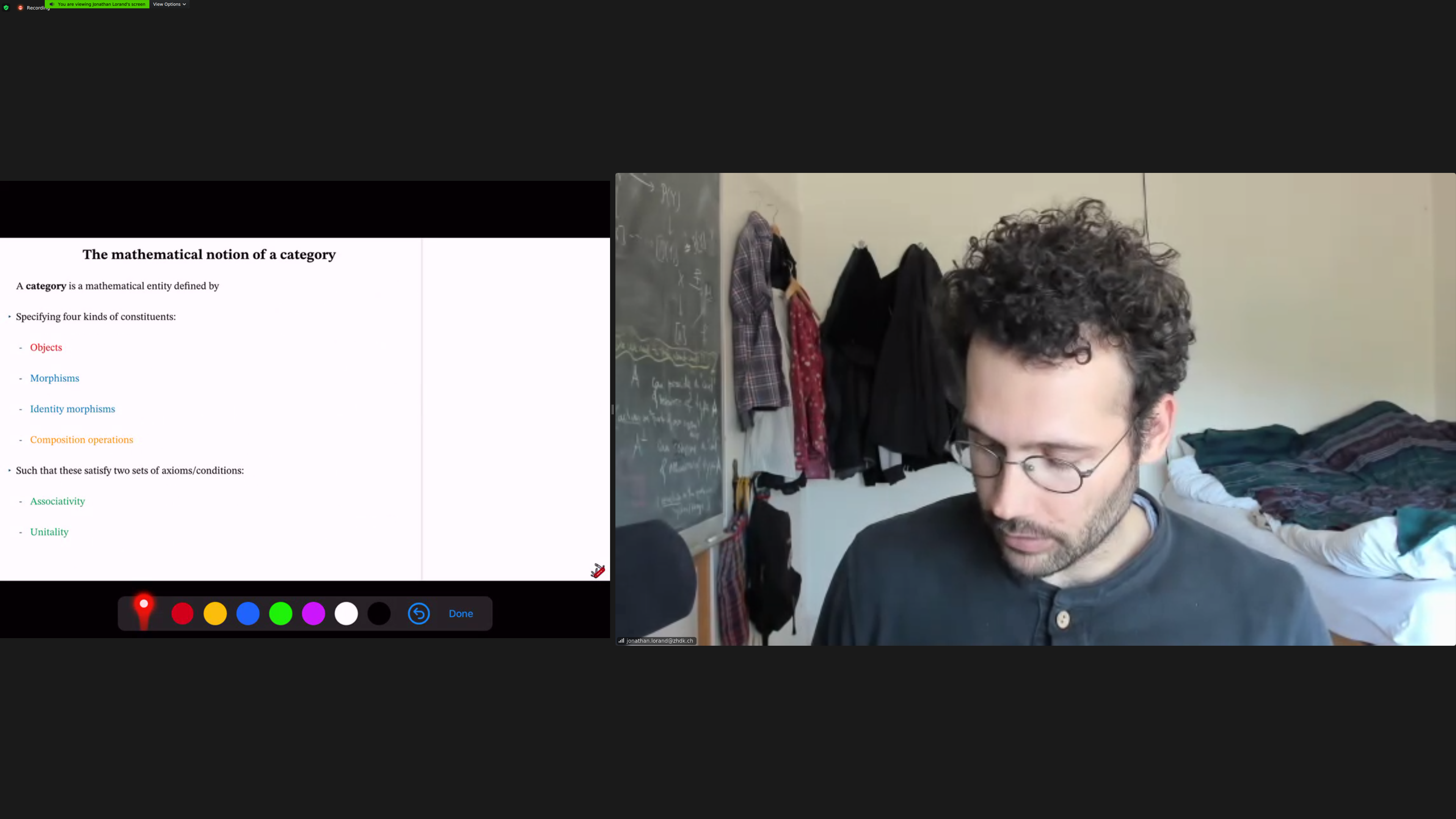
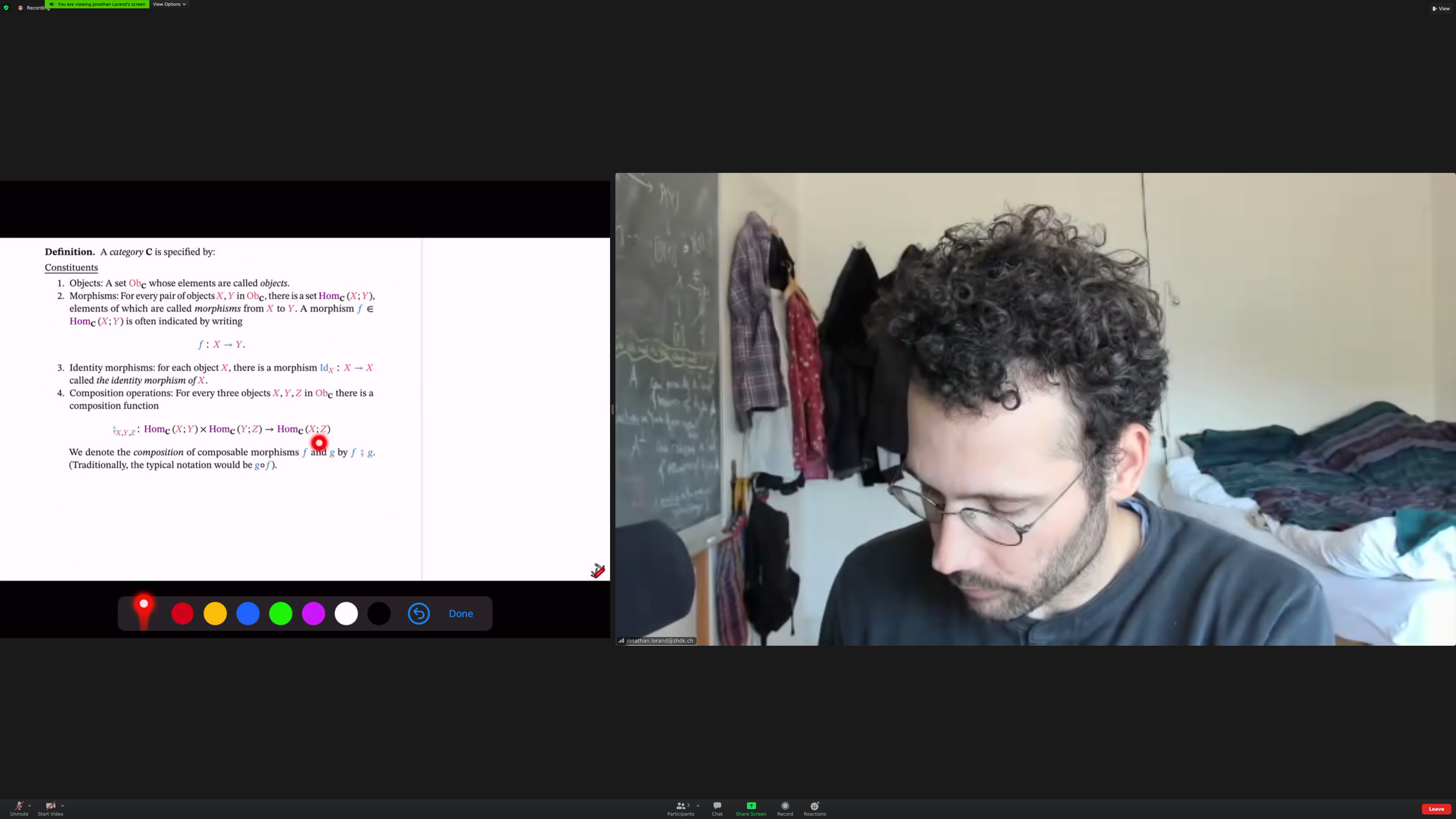
Mathematical notion of a category
Aside: I think most concepts had been introduced before except one?
"F is a morphism from X to Y":
Identity morphisms:
Composition:
Unitality: identity "works" (I think this was the concept I thought hadn't been defined previously):
The [[category of sets and functions]] plays a central role in category:
The [[category of plugs and chords]]:
The [[category of journeys]]:
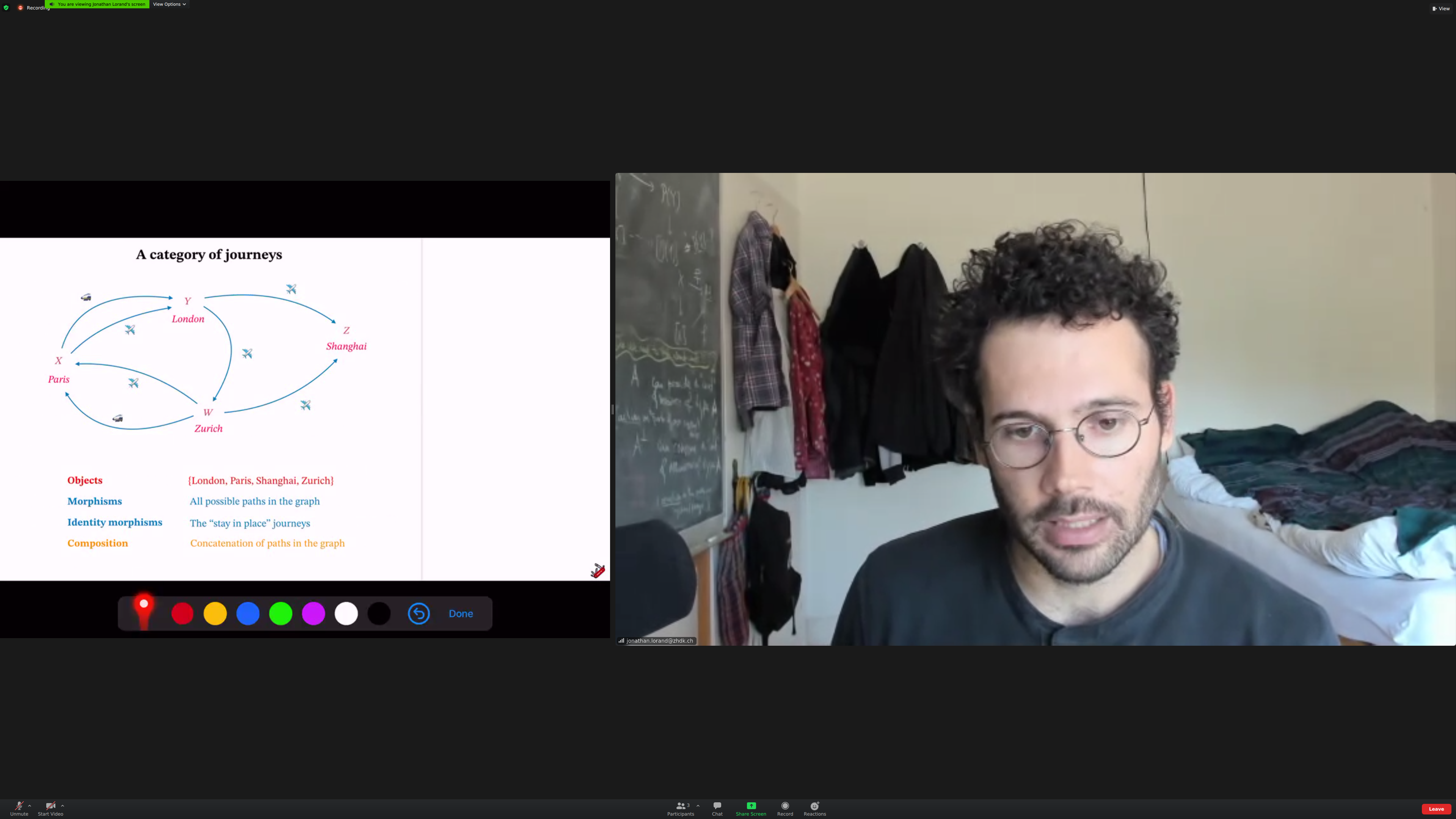
(Aside: some screenshots might be duplicate, they are likely from two moments that felt significant)
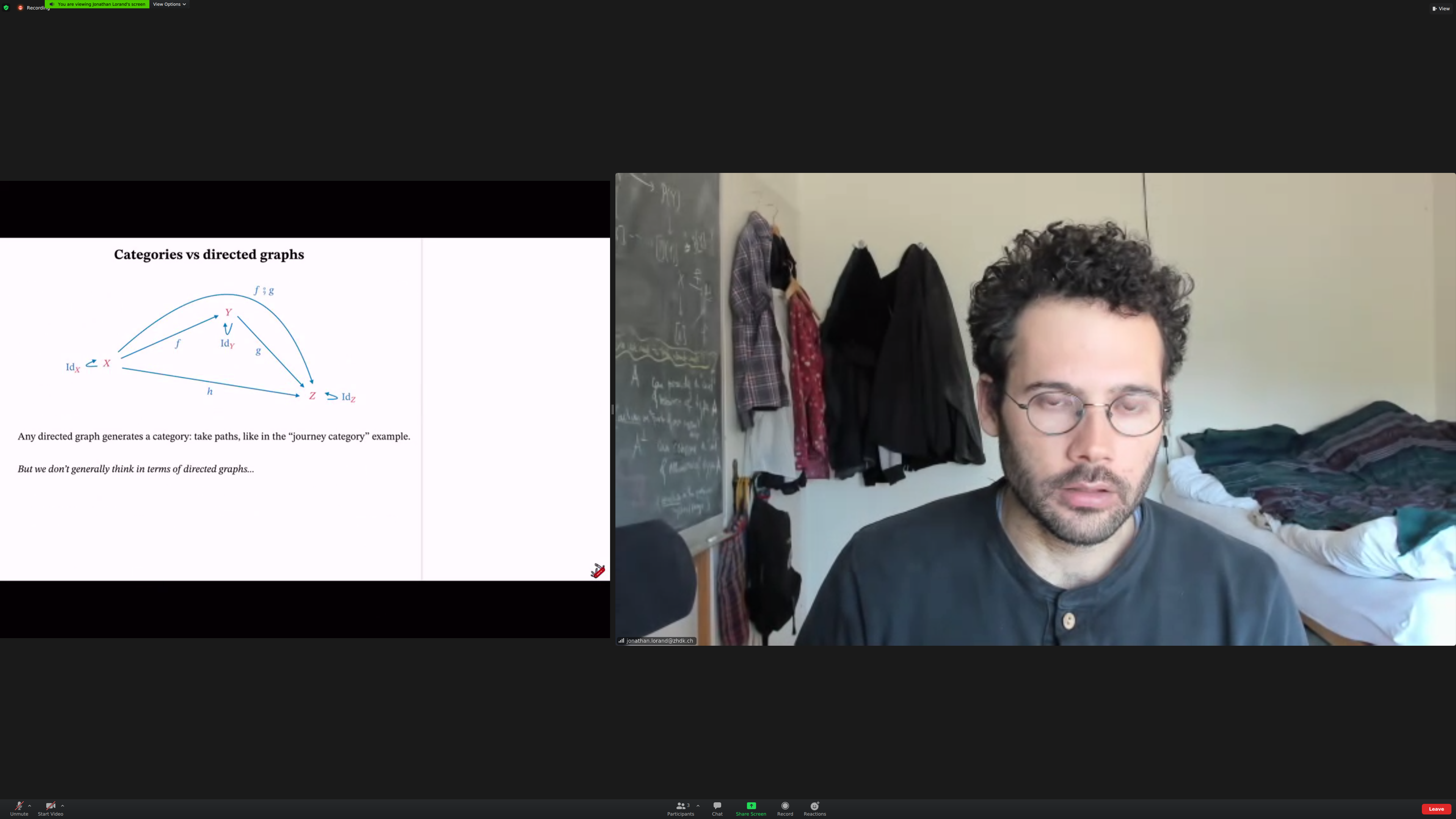
Any directed graph generates a category.
(Aside: a directed graph generates dependency trees.)
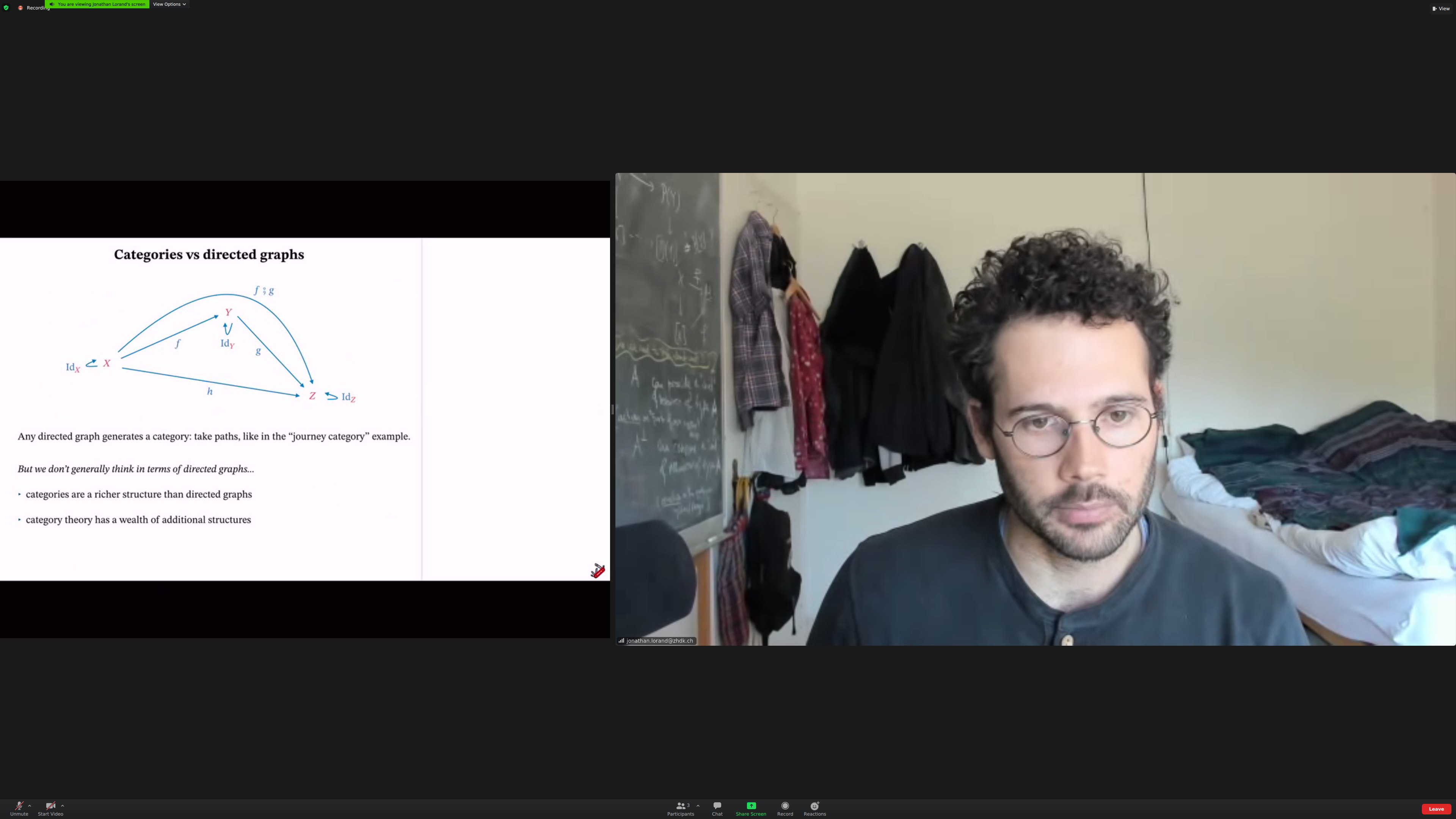
But categories are [[richer]] than [[directed graphs]], so they aren't used that much as such.
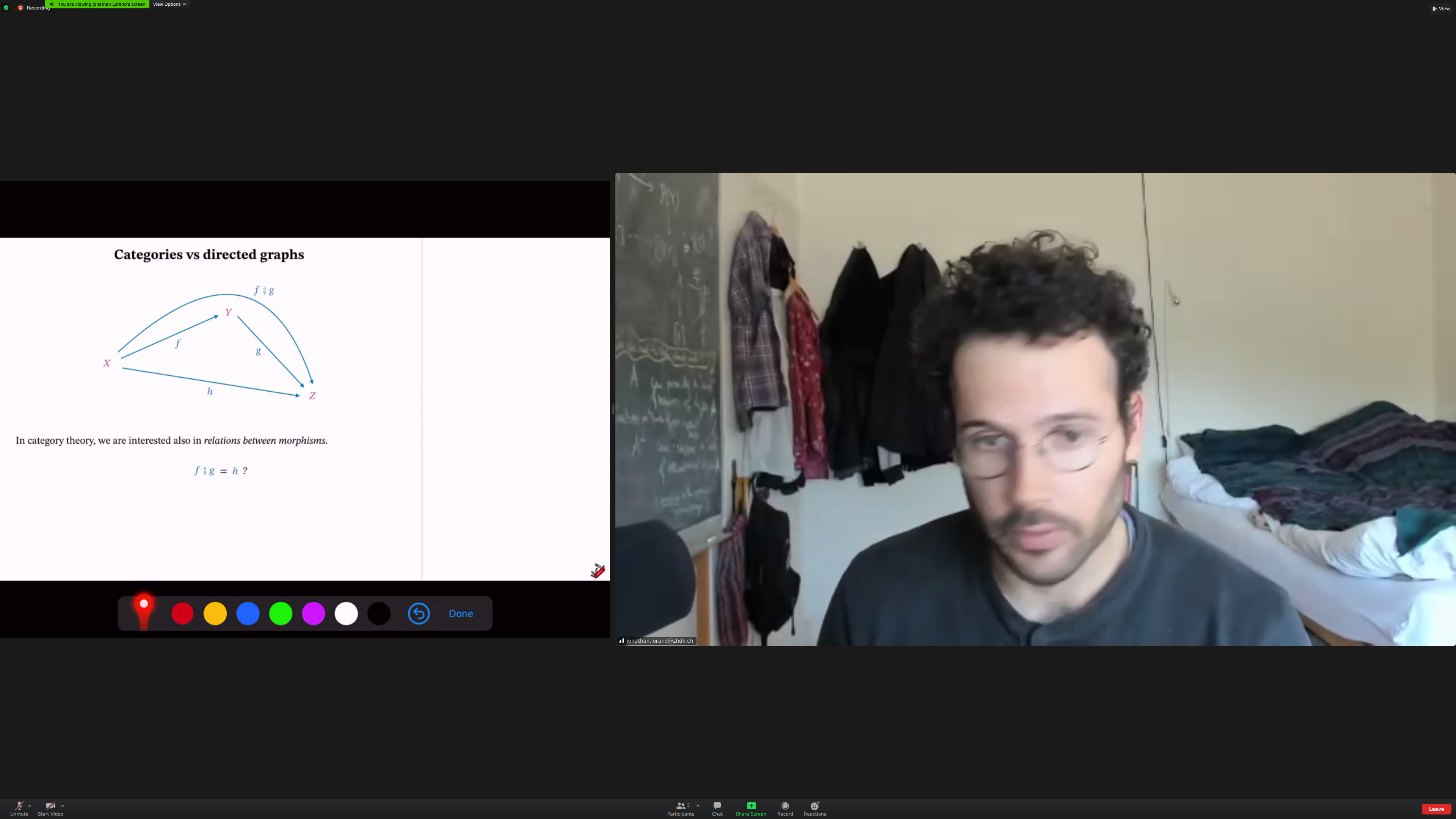
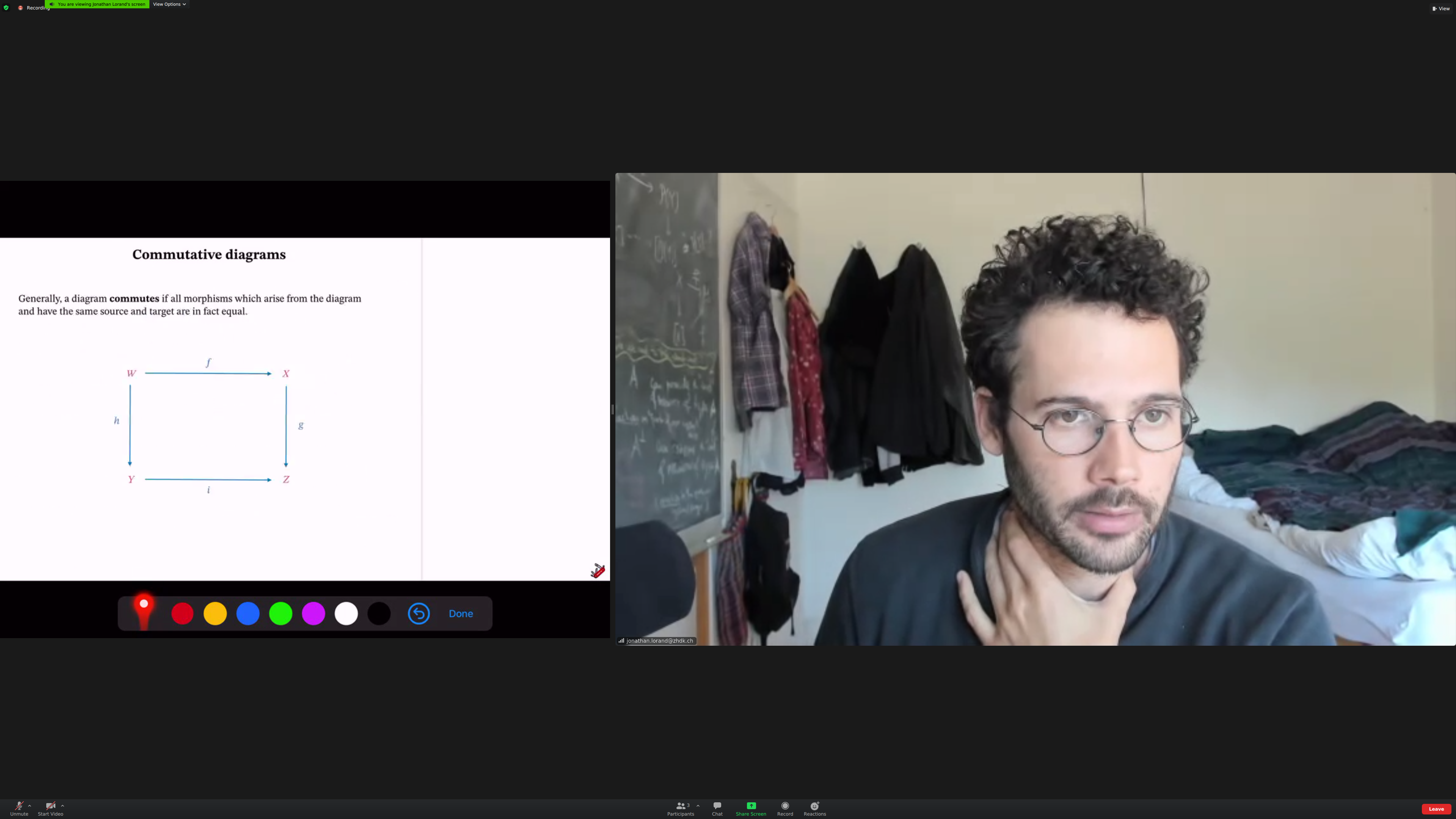
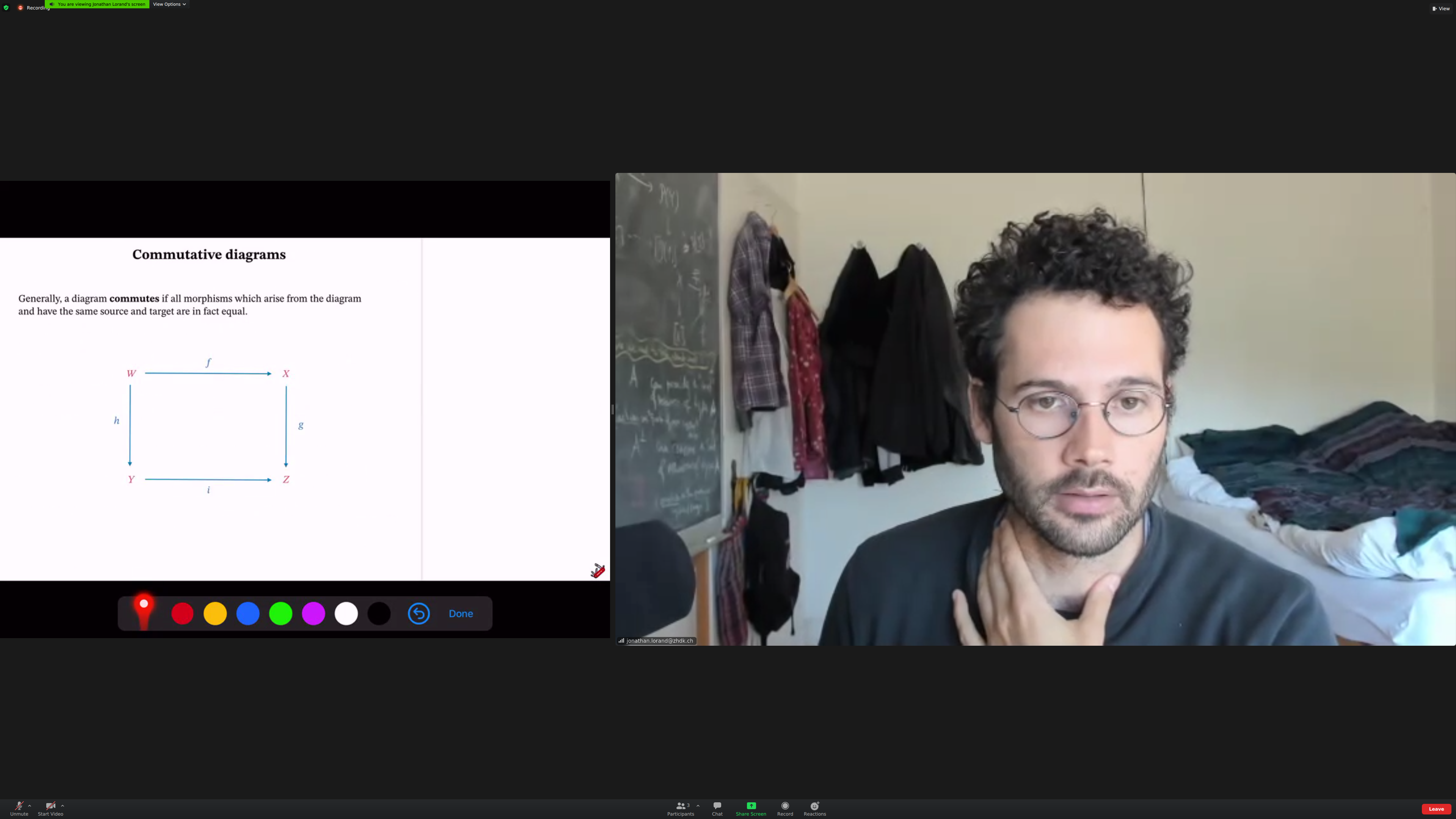
Category theory is interested in [[relations between morphisms]].
if f;g is equal to h, this diagram [[commutes]].
Aside: when you say 'if you compose' something, it'd be nice to have the right notation for the composition on screen.
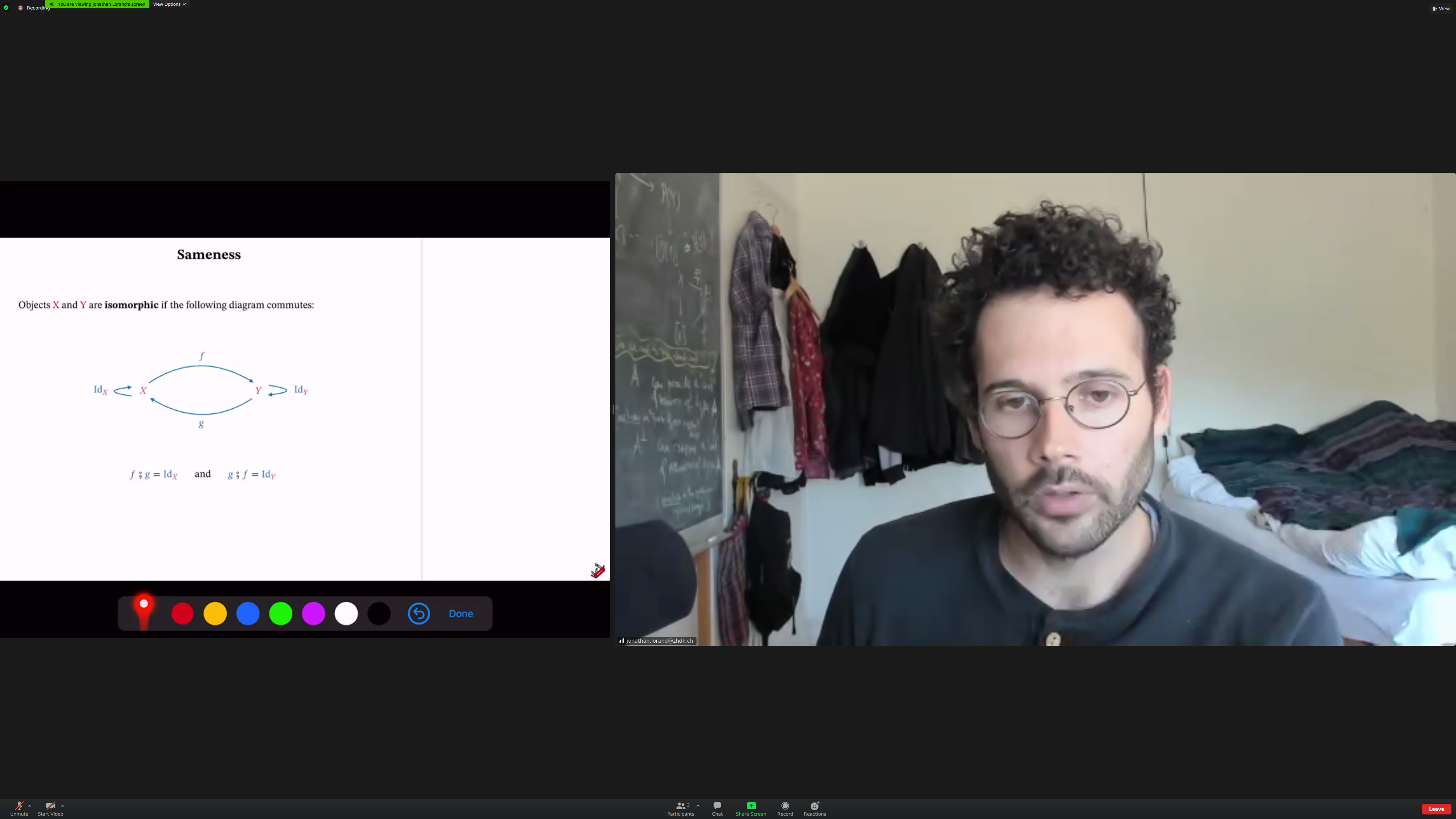
Sameness: [[isomorphism]]. Identity is equal to roundtrip.
(in the category of sets/functions, an isomorphism is equivalent to a [[bijection]]. in the category of topological spaces and continuous maps, it is a [[homeomorphism]])
A context.
(Aside: I needed more time in this slide).
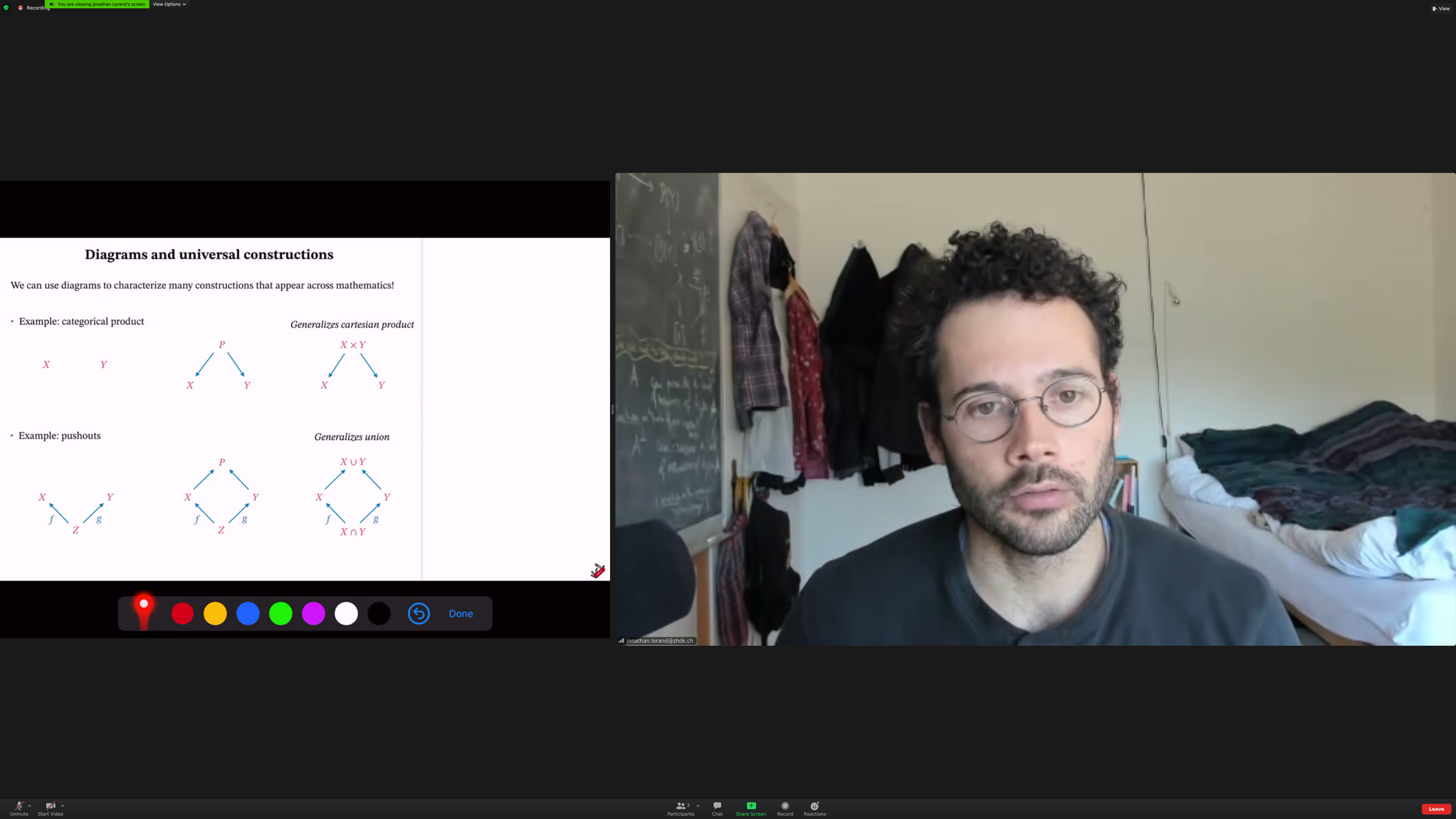
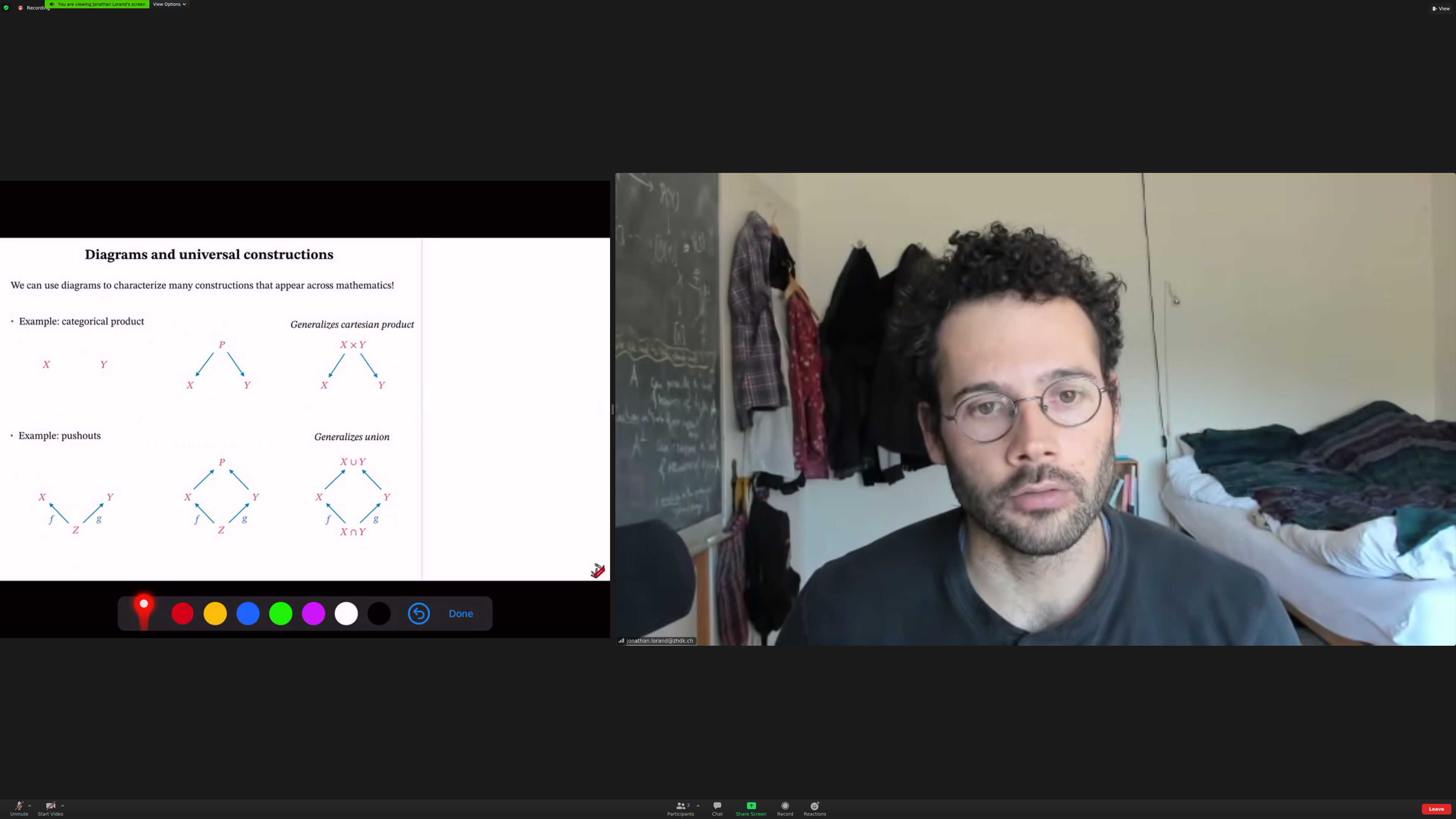
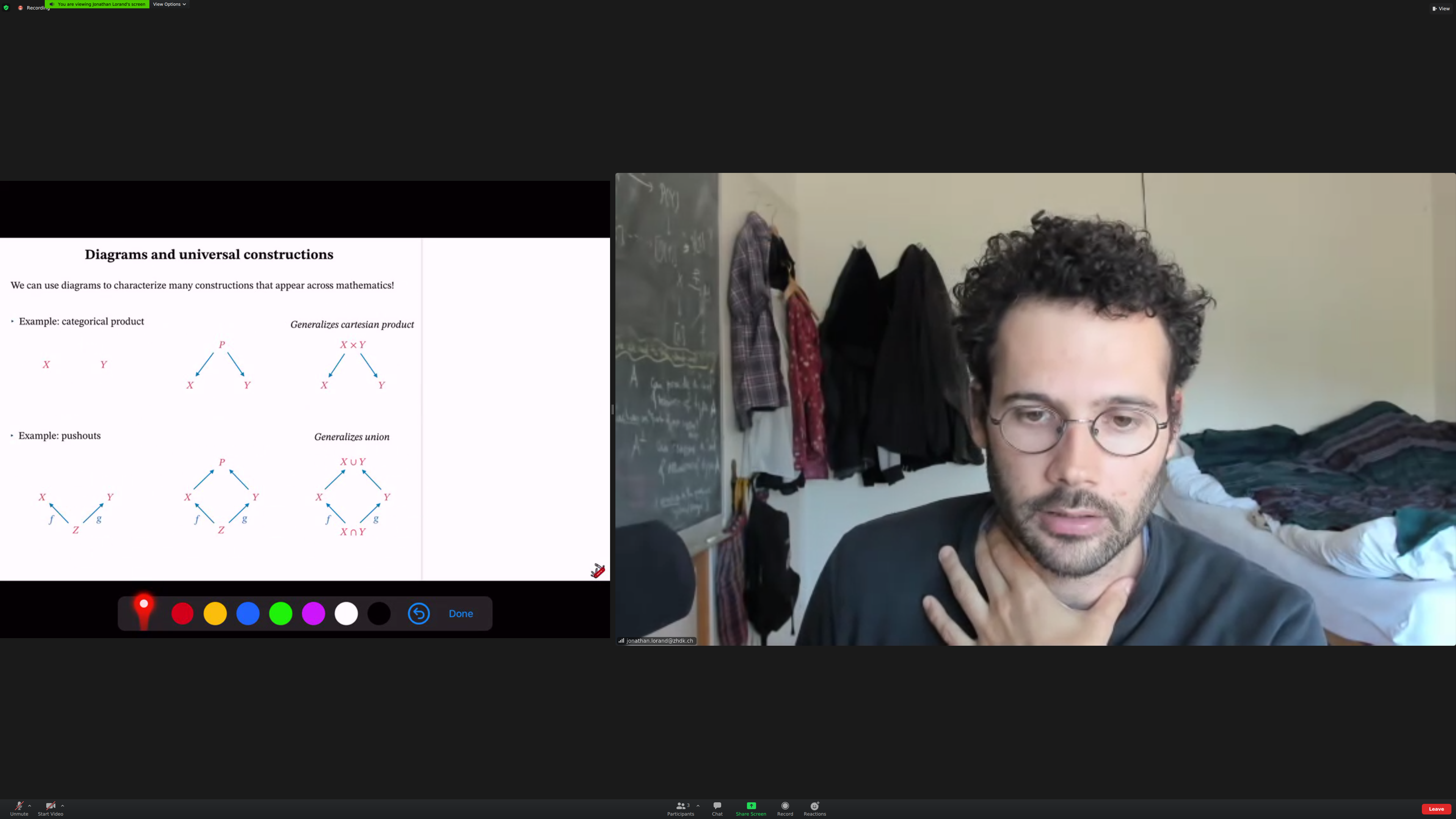
Contexts leads to [[universal constructions]] and [[universal properties]].
Example: [[categorical product]].
You start with objects, no morphisms. From the left diagram, you construct one with [[morphisms]]. In this one, we generalize cartesian product.
[[pushouts]] Using the information given by f and g, you [[integrate]] two objects (check).
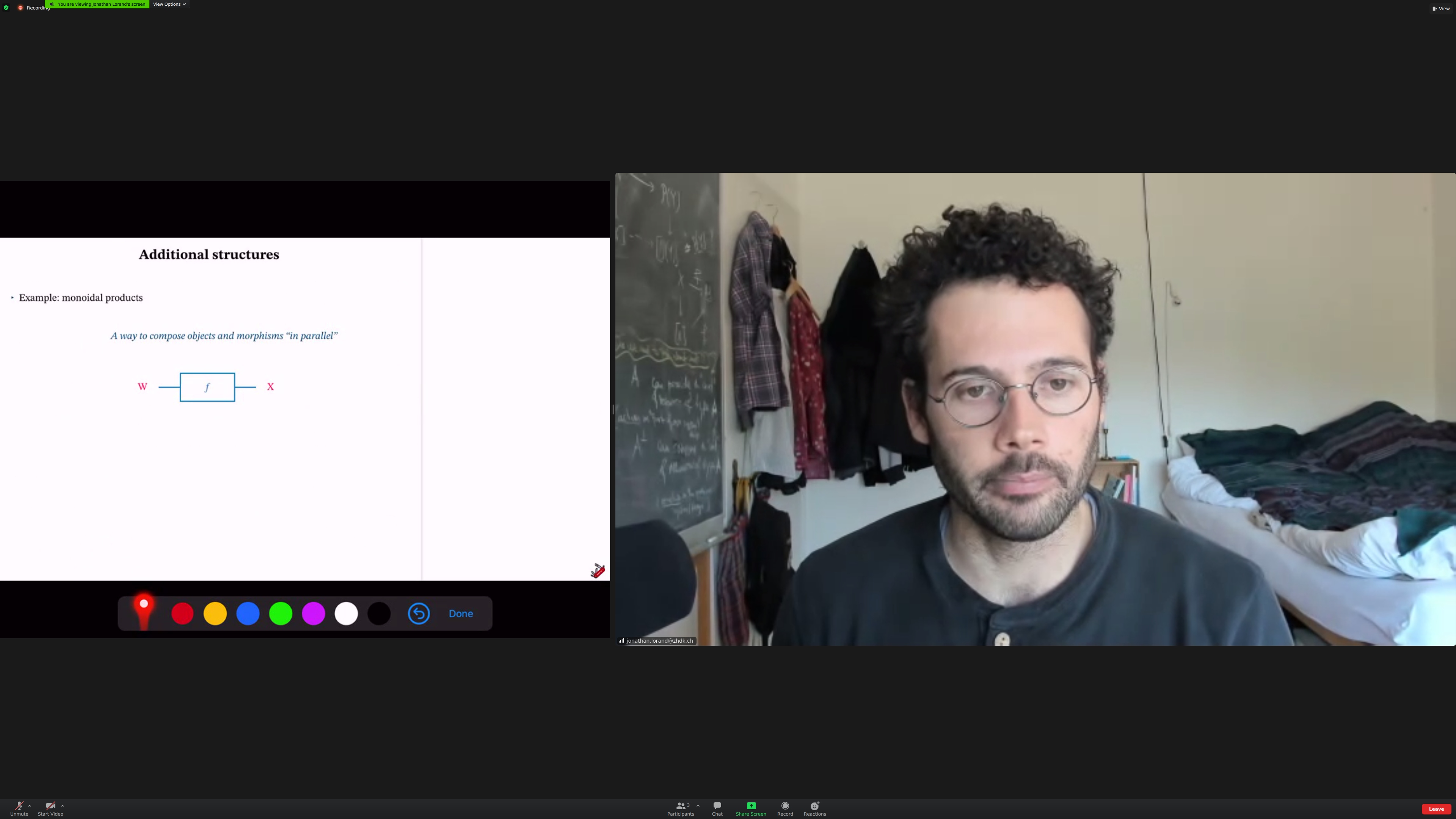
Additional structures: [[monoidal products]]. A way to compose objects and morphisms "in parallel".
(Aside: it would be nice to have original and post application of composition side by side or top to bottom).
(Aside: missing screenshot here, find in Pictures)
- First posted [[2021-01-01]]
-
Suggested program:
-
Step 1: Read the the paper [[A mathematical theory of co-design]], freely available here
- This has no category theory in it, and should be understandable without any prerequisites. I think that having a quick look at this paper will give you a sense if doing this mini-curriculum is something that would interest you. Another option is to skip this paper, and just do Step 2 (the 4th chapter in Step 2 covers some of the material from Step 1, but using category theory).
- Step 2: Read the first four chapters in the book [[Seven Sketches in Compositionality]], freely available here
-
Step 1: Read the the paper [[A mathematical theory of co-design]], freely available here
- public document at doc.anagora.org/category-theory
- video call at meet.jit.si/category-theory
2020 10 16
2020 10 17
2021 02 06
2021 05 30
2021 07 17
2021 07 28
2022 08 06
2023 01 23
2023 03 03
category
category theory basics
category theory for engineers
category theory for programmers
character class
jonathan the utopian
later
nordbrücke
pratyush
protopoi
research
simulation
steffen schuldenzucker